Matematické Fórum

malarad

Ahoj, mám ve skriptech příklad $(x^{2}+1)^{cos\pi x}$
takže v exponentu je $\cos$ $\pi$ $x$
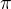
počítal jsem to tak, že pí a x je argumentem funkce cos. Zderivoval jsem to a vyšlo mi to dobře. Jak ale poznám, že x je skutečně součástí argumentu? Pro přehlednost by mohli psát argument do závorky. Třeba takto 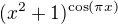$(x^{2}+1)^{\cos (\pi x)}$

délka mezery v učebnici u exponentu mezi cos pí a x je úplně stejná

Andrejka3 · 17. 11. 2015 12:24

↑ malarad:
Ahoj. Kdybych psala příklad já a chtěla bych mít argument cosinu jen pí, pak bych určitě napsala
$(x^{2}+1)^{x\cos\pi }$

jarrro · 17. 11. 2015 12:26 — Editoval jarrro (17. 11. 2015 12:27)

tak ako si to napisal je to
$(x^{2}+1)^{\cos{$\pi$}x}$
ine je
$(x^{2}+1)^{\cos{\pi{}x}}$
(medzera vie spraviť divy)

malarad · 17. 11. 2015 12:36

↑ jarrro:
ale v učebnici jsou mezery stejné-ostatně psal jsem to v posledním řádku- "délka mezery v učebnici u exponentu mezi cos pí a x je úplně stejná"

malarad · 17. 11. 2015 12:38

přesně je to v učebnici takto
//forum.matweb.cz/upload3/img/2015-11/60320_mezera.JPG

malarad · 17. 11. 2015 12:40

↑ Andrejka3:
to jsem si taky říkal, ale být to tak nemusí

jarrro · 17. 11. 2015 13:49

↑ malarad: no vidíš porovnaj
$$x^2+1$^{\cos{\pi{}x}}\text{ vs. }$x^2+1$^{\cos\pi x}$

byk7 · 17. 11. 2015 14:11

↑ jarrro: Já bych řekl, že to je to samé, protože nevím o žádném pravidle "přednosti" zohledňující mezery.

Jinak toto je věčný problém. Jak byste interpretovali zápis $4x\ :\ 3y$ ? Je to to samé co $4x:3y$ ? Mě na základní škole učili, že pokud jsou ve výrazu operace na stejné úrovni, pak se jde zleva doprava, tj. $4x:3y=4\cdot x:3\cdot y=\frac{4xy}{3}$ .

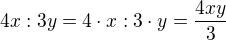Anebo problém, který se "nedávno" řešil, čemu je rovno 6÷2(1+2)? (Dle mého není o čem diskutovat a výsledek je 9.)

Prostě, pokud se chceš vyhnout jakýmkoliv nejasnostem, používej(te) závorky a radši víc než míň. :)

Akojeto · 17. 11. 2015 14:45

↑ byk7:

Presne tak.

Brano · 17. 11. 2015 20:15 — Editoval Brano (17. 11. 2015 20:30)

↑ byk7:
v tomto pripade na to existuje konsezus.
nasobenie kde pises bodku a delenie kde pises dvojbodku maju rovnaku prioritu, ale nasobenie bez bodky ma vyssiu prioritu teda $2a:3b=\frac{2a}{3b}$ avsak $2a:3\cdot b=\frac{2a}{3}b$
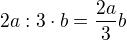
(lenze ako to uz byva nie vzdy sa vsetky konsenzy do bodky dodrziavaju :D )

ako je to s prioritou nasobenia bez bodky a aplikacie funkcie mi nie je az tak jasne, ale velmi caso sa pouziva
$\text{fun}\,ab$ v zmysle $\text{fun}(ab)$ - tak by som povedal, ze ma teda prednost aj pred aplikaciou; ale treba si na to proste davat pozor a snad aj vo vlastnych textoch byt radsej slusny a tu zatvorku tam napisat; ale ako nutnost by som to nevidel - ved kto by uz pisal 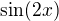$\sin(2x)$ ked moze napisat 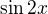$\sin 2x$ , nie?

vanok · 17. 11. 2015 20:24

Poznamka.
Aj ked su mozno dohody, taketo delikatne situacie by som pisal zo zatvorkamy.
( alebo by som pouzil opacnu polsku notaciu https://en.m.wikipedia.org/wiki/Reverse_Polish_notation) mozno to niekto vola aj postfixove oznacenie?

Brano · 17. 11. 2015 20:34

↑ vanok:
programoval som v lispe, ktory pouziva polsku (prefixovu) notaciu a teda niekedy je to otrava (lisp uznava iba uplne uzatvorkovane vyrazy, lebo napr take + nema jasne dany pocet argumentov a nascita uplne vsetko co je za nim)

vanok · 17. 11. 2015 20:49

↑ Brano:
TO je pravda ze, z tym znacenym je tiez gymnastika.... Ale aj tak som ako ty, radcej zatvorky aj navyse ako napisat nieco co moze byt spatne interpretovane.

Matematické Fórum

#1 17. 11. 2015 12:19 — Editoval malarad (17. 11. 2015 12:20)

jak poznám, že se jedná o argument funkce

#2 17. 11. 2015 12:24

Re: jak poznám, že se jedná o argument funkce

#3 17. 11. 2015 12:26 — Editoval jarrro (17. 11. 2015 12:27)

Re: jak poznám, že se jedná o argument funkce

#4 17. 11. 2015 12:36

Re: jak poznám, že se jedná o argument funkce

#5 17. 11. 2015 12:38

Re: jak poznám, že se jedná o argument funkce

#6 17. 11. 2015 12:40

Re: jak poznám, že se jedná o argument funkce

#7 17. 11. 2015 13:49

Re: jak poznám, že se jedná o argument funkce

#8 17. 11. 2015 14:11

Re: jak poznám, že se jedná o argument funkce

#9 17. 11. 2015 14:45

Re: jak poznám, že se jedná o argument funkce

#10 17. 11. 2015 20:15 — Editoval Brano (17. 11. 2015 20:30)

Re: jak poznám, že se jedná o argument funkce

#11 17. 11. 2015 20:24

Re: jak poznám, že se jedná o argument funkce

#12 17. 11. 2015 20:34

Re: jak poznám, že se jedná o argument funkce

#13 17. 11. 2015 20:49

Re: jak poznám, že se jedná o argument funkce

Zápatí