Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » trojny integral substitucia polarne sfericke cylindricke suradnice (TOTO TÉMA JE VYŘEŠENÉ)
#1 21. 11. 2015 21:09
trojny integral substitucia polarne sfericke cylindricke suradnice
zdravim,
prosim Vas o vysvetlenie a ozrejmenie si niektorych pojmov, ponukam rieseny priklad 
prosim Vas, ten uhol  vždy závisí od toho
vždy závisí od toho 
 Dobre som to vyargumentoval?
Dobre som to vyargumentoval?
Resp. ked mi vysla podmienka  Vzdy to bude od 0 ?
Vzdy to bude od 0 ?
A tak teda musi byt  vzdy od 0 po
vzdy od 0 po  ?
?
Ďakujem.
Offline
- (téma jako vyřešené označil(a) fyzika)
#2 22. 11. 2015 08:54
Re: trojny integral substitucia polarne sfericke cylindricke suradnice
↑ fyzika:
Dobrý den.
Podle mě postupujete správně. Nejsem si jistý, zda doplňujícím dotazům správně rozumím:
Pokud je v definici transformace  , pak bude zřejmě vždy r >= 0; ovšem s ohledem na periodicitu goniometrických funkcí můžete mít meze v integrálu třeba
, pak bude zřejmě vždy r >= 0; ovšem s ohledem na periodicitu goniometrických funkcí můžete mít meze v integrálu třeba 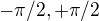 .
.
Pokud se tedy nemýlím.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » trojny integral substitucia polarne sfericke cylindricke suradnice (TOTO TÉMA JE VYŘEŠENÉ)
