Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#51 27. 05. 2009 07:26
- vonSternberk
- Příspěvky: 269
- Reputace: 0
Re: Logaritmická rovnice
jj;-)
muzete poradit:
ja dal počital:
a teďko nevím zda-li mám dělit celou rovnici 2 nebo jestli můžu odečíst ty logartimy?
Offline
#55 27. 05. 2009 15:02
- vonSternberk
- Příspěvky: 269
- Reputace: 0
Re: Logaritmická rovnice
muzete zkontrolovat/poradit:
ja pocital:


a dalej nevím:(
Offline
#58 27. 05. 2009 15:16
Re: Logaritmická rovnice
↑ gadgetka:
HH máme to na chlup stejné :-)
Ale přesto si dovolím poznámku. Ten argument logaritmu je opardvu vhodné psát do závorky, aby byl jasný. protože pokud máš logx bez závorky a pak tam je logx-2 tak to pak není jasné.
oo^0 = 1
Offline
#59 27. 05. 2009 15:19
- vonSternberk
- Příspěvky: 269
- Reputace: 0
Re: Logaritmická rovnice
jj je to dobře akorát nerozumím předposlednímu kroku, když mi vyjde:
tak by potom mělo bejt 

Offline
#60 27. 05. 2009 15:25
Re: Logaritmická rovnice
↑ vonSternberk:  by bylo rovno
by bylo rovno  , kdyby melo byt
, kdyby melo byt  . Ovsem to tady neni. Tady je
. Ovsem to tady neni. Tady je  , coz je neco jineho.
, coz je neco jineho.
Offline
#61 27. 05. 2009 16:34
- vonSternberk
- Příspěvky: 269
- Reputace: 0
Re: Logaritmická rovnice
dík za vysvětlení
muzete mi řict kde jsem udělal chybu v tomto příkladu:
pocital jsem


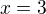
Offline
#62 27. 05. 2009 16:38 — Editoval Chrpa (27. 05. 2009 16:39)
#65 27. 05. 2009 17:13
- vonSternberk
- Příspěvky: 269
- Reputace: 0
Re: Logaritmická rovnice
muzete zkontrolovat toto:
ja pocital:

 , ale ma vyjit
, ale ma vyjit 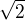
Offline
#68 27. 05. 2009 17:27
- vonSternberk
- Příspěvky: 269
- Reputace: 0
Re: Logaritmická rovnice
kde jsem udělal chybu tady:
ja pocitam

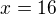
Offline
#71 27. 05. 2009 17:37
- vonSternberk
- Příspěvky: 269
- Reputace: 0
Re: Logaritmická rovnice
a v tomto příkladě:
mě vyšlo:
(x+2)(x+3), ale ve výsledku je napsáno, že rovnice nemá řešení, jaktože?! Vždyť i podmínky sedijou
Offline
#73 27. 05. 2009 18:15
- vonSternberk
- Příspěvky: 269
- Reputace: 0
Re: Logaritmická rovnice
jaktože, vždyť  je
je  dále
dále  a
a  , ne?!
, ne?!
Offline
#75 27. 05. 2009 18:50
- vonSternberk
- Příspěvky: 269
- Reputace: 0
Re: Logaritmická rovnice
jo díky zase ty podmínky...chtěl bych pomoct jeste s tímto: 
...já jsem postupoval: , ale dál jsem nevěděl jak se zbavit logartimu!:(
, ale dál jsem nevěděl jak se zbavit logartimu!:(
Offline

![kopírovat do textarea $\sqrt[3]{5}$](/mathtex/71/71f4d0d7fc3f82d9e9953cac1cb1b28e.gif)

![kopírovat do textarea $\log x^3=\log10-\log2\nl\log x^3=\log \frac{10}{2}\nlx^3=5\nlx=\sqrt[3]{5}$](/mathtex/61/61d9dbdcb10f4f791c73f5a46c275e35.gif)





 :-)
:-)



