Matematické Fórum

Mara321 · 16. 05. 2009 21:25

Dostali jsme příklad - Upravte: Cos2x/sinx+cosx . Zkoušel jsem to ruzně upravovat podle různých goniom. vzorců a nedošel jsem k žádnému pěknému výsledku. Dík za případnou pomoc.

Cartmen · 16. 05. 2009 21:29

cos^2x - sin^2x/sinx+cosx = (cosx - sinx).(cosx+sinx)/sinx+cosx = cosx-sinx

Snad to je dobre ...

Mara321

To jsem nevěděl že se to muže upravit podle vzorce x^2 - y^2=(x-y)(x+y) Ted je otazka, ktery vysledek je dobře. Jestli od Cartmena "cosx - sinx" anebo od Alivendese "sinx-cosx"..
Ja bych řek že od Cartmena, bo Cos^2x - Sin^2x by mel byt po upravě (Cosx-Sinx)*( atd....) na ne (Sinx-Cosx)*(...+...) ne?.

marnes · 16. 05. 2009 21:50

↑ Mara321:Od cartmen

Alivendes · 16. 05. 2009 21:54

ano pardon převedl jsem to špatně sem unavenej :D

Cartmen · 17. 05. 2009 19:35

Ta matura snad neco se mnou udelala:D

vonSternberk · 30. 05. 2009 11:42

jak byste řešili toto:
kolik průsečíků má funkce f:y=cotgx s přímkou y=-3 na intervalu $(0;\pi)$

marnes · 30. 05. 2009 11:49

↑ vonSternberk:Zkus si třeba načrtnout pro představu graf fce cotg a přímku y =-3. Jinak řešíš malou rovnici

vonSternberk · 30. 05. 2009 11:56

no kdyby to bylo tak tak y=-3 nemá žádnej průsečík s fcí cotg, protože ta je pouze do y=(-1;1)

marnes · 30. 05. 2009 12:03

↑ vonSternberk:Nene, sin a cos je (-1;1), tg a cotg je -oo;oo. Najdi si někde, jak vypadají grafy

halogan · 30. 05. 2009 12:04

Cotg není cos. Cotg má obor hodnot R.

Chrpa · 30. 05. 2009 12:13

↑ vonSternberk:
Tady máš nástroj na sestrojení grafu:
http://user.mendelu.cz/marik/maw/index.php?l
Najedeš na funkce a do políčka dáš cotg(x)
x min =0 x max = necháš.
a dáš odeslat.
Vykreslí ti to graf cotg(x)

vonSternberk · 30. 05. 2009 15:20

jj..jeste taková malá otázka je-li sinx=1, pak sin2x=?

gadgetka

$\sin x=1\qquad /^2\nl\sin^2 x=1\nl1-\cos^2 x=1\nl\cos^2 x=0\nl\cos x=0\nl\sin 2x=2\sin x\cos x=2\cdot 1\cdot 0=0$

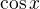(to, že $\cos x$ je rovno v tomto případě nule, je zřejmé i ze vzorce $\sin^2 x+\cos^2 x=1$ )

Matematické Fórum

#1 16. 05. 2009 21:25

goniometrická funkce

#2 16. 05. 2009 21:29

Re: goniometrická funkce

#3 16. 05. 2009 21:48 — Editoval Mara321 (16. 05. 2009 21:49)

Re: goniometrická funkce

#4 16. 05. 2009 21:50

Re: goniometrická funkce

#5 16. 05. 2009 21:54

Re: goniometrická funkce

#6 17. 05. 2009 19:35

Re: goniometrická funkce

#7 30. 05. 2009 11:42

Re: goniometrická funkce

#8 30. 05. 2009 11:49

Re: goniometrická funkce

#9 30. 05. 2009 11:56

Re: goniometrická funkce

#10 30. 05. 2009 12:03

Re: goniometrická funkce

#11 30. 05. 2009 12:04

Re: goniometrická funkce

#12 30. 05. 2009 12:13

Re: goniometrická funkce

#13 30. 05. 2009 15:20

Re: goniometrická funkce

#14 30. 05. 2009 17:29 — Editoval gadgetka (30. 05. 2009 17:31)

Re: goniometrická funkce

Zápatí