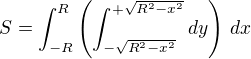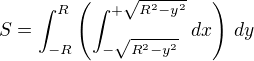Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Fyzika
- » Moment setrvacnosti, integrace v Kartezskych (TOTO TÉMA JE VYŘEŠENÉ)
#1 12. 12. 2015 10:32
Moment setrvacnosti, integrace v Kartezskych
Ahoj, priklad ma zadani: vypoctete moment setrvacsnoti homogeni koule o polomeru R a hmotnosti M, vzhledem k ose prochazejici jejim hmotnym stredem.
Priklad se samozrejme resi integraci, dle vztahu: 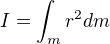
Priklad jsem vyresil, pri integraci pres sfericke souradnice. Chtel bych se to vsak naucit i pres kartezske souradnice. Nastinim muj postup, ktery nevedkl k uspechu.  (jeste zde chybi hustota ale tu jsem BUNO vynechal)
(jeste zde chybi hustota ale tu jsem BUNO vynechal)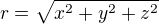
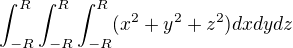
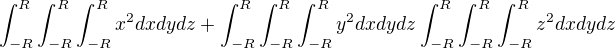
Coz nevede ke spravnemu reseni. Prosim o radu kde delam chybu.
pozn. spravne reseni je 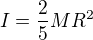
Dik y.
Offline
- (téma jako vyřešené označil(a) Ondrik_B)
#2 12. 12. 2015 11:47
Re: Moment setrvacnosti, integrace v Kartezskych
↑ Ondrik_B:
Dobrý den.
Myslím, že jste uvedeným integrálem mohl (asi) spočítat moment setrvačnosti krychle.
Řekl bych, že moment setrvačnosti koule by se zřejmě počítal integrálem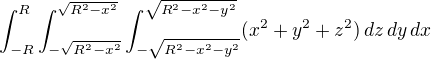
což bych tedy v kartézských souřadnicích počítat nechtěl.
Pokud se tedy nemýlím.
Offline
#3 12. 12. 2015 12:17
Re: Moment setrvacnosti, integrace v Kartezskych
↑ Jj:
Ano to me taky napadlo, ze to bude spis krychle. Ale nenapadlo me, jak ty meze urcit. (od R k R mi prislo intuitivni) Jak jste prisel na tyto meze. (O samotnou integraci mi nejde, chci spis pochopit to 'sestaveni' integralu)
Offline
#4 13. 12. 2015 17:06 — Editoval Jj (13. 12. 2015 17:09)
Re: Moment setrvacnosti, integrace v Kartezskych
↑ Ondrik_B:
Určení mezí na zjedodušeném příkladu - plocha kruhu o poloměru R:
Případnou změnu pořadí integrace by bylo nutno promítnou do příslušných změn mezí intetgrace.
Pokud se tedy nemýlím.
Offline
Stránky: 1
- Hlavní strana
- » Fyzika
- » Moment setrvacnosti, integrace v Kartezskych (TOTO TÉMA JE VYŘEŠENÉ)


 , pak obsah kruhu = přibližně součtu všech těchto plošek. Při součtu plošek ve svislém směru máme obsah zvýrazněného sloupce, ve vodorovném směru sečteme obsahy všech takto vzniklých sloupců (ty mají v návaznosti na svou polohu různou výšku).
, pak obsah kruhu = přibližně součtu všech těchto plošek. Při součtu plošek ve svislém směru máme obsah zvýrazněného sloupce, ve vodorovném směru sečteme obsahy všech takto vzniklých sloupců (ty mají v návaznosti na svou polohu různou výšku).