Matematické Fórum

Crashatorr

Zdravím mohl by se někdo kouknout na můj postup a říct jestli je to dobře?

Dokaž, že Riemannova zeta funkce 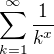$\sum_{k=1}^{\infty }\frac{1}{k^{x}}$ je spojitá pro x>1 a má na této množině spojité derivace všech řádů.

Pomocí integrálního kritéria bych dokázal že je bodově spojitá pro x>1, pak zde přikládám vyfocený postup.
Potřebuju dokázat stejnoměrnou konvergenci, to jsem udělal a pak za předpokladu že funkce 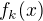$f_{k}(x)$ jsou spojité na oboru stejnoměrné konvergence je i zeta funkce spojitá.
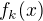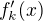Dále jsem derivoval funkční řadu a rozhodl o její bodové a stejnoměrné konvergenci, opět díky tomu, že funkce $f_{k}(x)$ a $f_{k}'(x)$ má spůojité derivace všech řádů

Autor skryl část textu. Zobrazit/skrýt!

Crashatorr · 13. 12. 2015 12:38

Věděl by někdo?

Pavel · 13. 12. 2015 16:43 — Editoval Pavel (13. 12. 2015 16:44)

↑ Crashatorr:

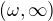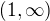To, že řada konverguje stejnoměrně na $(\omega,\infty)$ pro libovolné $\omega>1$ , neznamená, že konverguje stejnoměrně na $(1,\infty)$ . Tam řada konverguje pouze lokálně stejnoměrně. Nicméně i toto ke spojitosti Riemannovy funkce stačí.

Crashatorr · 13. 12. 2015 16:48

↑ Pavel:
Co by bylo třeba tedy dodat, když bych nevěděl, že lokální stejnoměrná konvergence pro spojitost Riemannovy funkce stačí?

Matematické Fórum

#1 12. 12. 2015 16:09 — Editoval Crashatorr (12. 12. 2015 16:09)

Riemannova zeta funkce

#2 13. 12. 2015 12:38

Re: Riemannova zeta funkce

#3 13. 12. 2015 16:43 — Editoval Pavel (13. 12. 2015 16:44)

Re: Riemannova zeta funkce

#4 13. 12. 2015 16:48

Re: Riemannova zeta funkce

Zápatí