Matematické Fórum

Crashatorr

Zdravím, poprosil bych jen o kontrolu úvahy

Urči součet funkční řady 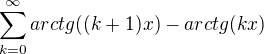$\sum_{k=0}^{\infty } arctg((k+1)x)-arctg(kx)$ a rozhodni o její konvergenci

Když si řadu rozepíšu 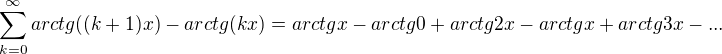$\sum_{k=0}^{\infty } arctg((k+1)x)-arctg(kx)=arctgx-arctg0+arctg2x-arctgx+arctg3x-...$
tak vidím, že arctg 0=0 a poté se mi tam začnou členy řady odečítat takže bych mohl pro velké k uvažovat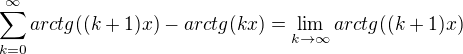
$\sum_{k=0}^{\infty } arctg((k+1)x)-arctg(kx)=\lim_{k\to\infty }arctg((k+1)x)$
kde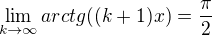
$\lim_{k\to\infty }arctg((k+1)x)=\frac{\pi }{2}$

a typ konvergence stačí celou zadanou řadu ohraničit konstantní funkcí pi/2, čili by měla konvergovat stejnoměrně na (0,1) no a v nule se dostaneme k součtu samých nul takže tu tam nehodím a 1 ano takže konverguje stejnoměrně na (0,1>

OndrasV · 12. 12. 2015 18:06

↑ Crashatorr: K stejnému výsledku jsem došel i já.

Crashatorr · 12. 12. 2015 18:20

↑ OndrasV:
Díky za kontrolu.

Pavel · 12. 12. 2015 19:35 — Editoval Pavel (12. 12. 2015 19:37)

↑ Crashatorr:

Obávám se, že to není dobře. V okolí bodu x=0 částečné součty nekonečné řady nekonvergují stejnoměrně k hodnotě 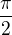$\frac{\pi}2$ . Interval 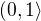$(0,1\rangle$ je špatně. Navíc mi není jasné, proč jsou z oboru konvergence vyloučena čísla $x>1$ a dále proč se neuvažují čísla $x<0$ .

Crashatorr · 12. 12. 2015 19:53

↑ Pavel:
To se omlouvám zapomněl jsem na začátku dopsat podmínku 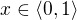$x\in\langle0,1\rangle$
A ten obor stejnoměrné konvergence je tedy špatně?

Pavel · 12. 12. 2015 20:12

↑ Crashatorr:

Aha, tak to je jiná. Nicméně ten obor stejnoměrné konvergence je opravdu špatně. Na intervalu 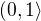$(0,1\rangle$ konverguje posloupnost funkcí pouze lokálně stejnoměrně, nikoli stejnoměrně.

Ta nula tam dělá problém - bohužel nestačí ji pouze vyloučit ze zadaného intervalu. Je nutné uvažovat interval 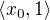$\langle x_0,1\rangle$ , kde $x_0\in(0,1)$ . Na něm pak bude posloupnost stejnoměrně konvergentní.

Crashatorr · 12. 12. 2015 20:18

↑ Pavel:
Jo myslím, že to chápu, díky za reakci.

Matematické Fórum

#1 12. 12. 2015 17:44 — Editoval Crashatorr (12. 12. 2015 17:48)

Součet a typ konvergence řady

#2 12. 12. 2015 18:06

Re: Součet a typ konvergence řady

#3 12. 12. 2015 18:20

Re: Součet a typ konvergence řady

#4 12. 12. 2015 19:35 — Editoval Pavel (12. 12. 2015 19:37)

Re: Součet a typ konvergence řady

#5 12. 12. 2015 19:53

Re: Součet a typ konvergence řady

#6 12. 12. 2015 20:12

Re: Součet a typ konvergence řady

#7 12. 12. 2015 20:18

Re: Součet a typ konvergence řady

Zápatí