Matematické Fórum

Mauz · 16. 12. 2015 18:55 — Editoval Mauz (16. 12. 2015 18:56)

Zadání:
Nechť A je matice typu p*q (p řádků, q sloupců) nad tělesem T.
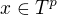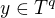Dokažte, že hodnost matice A je rovná jedné právě tehdy, když existují nenulové aritmetické vektory $x\in T^{p}$ a $y\in T^{q}$ takové, že $A=xy^{T}$ .

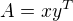Co z toho plyne:
1) matice má po gausově eliminaci jeden nenulový řádek (z hodnosti rovné 1), pro součin takových aritmetických vektorů se rovnající matici A.

Dál už to jaksi nechápu :(

Jaký vztah tam platí? Co chci dokázat?

Díky

OndrasV · 16. 12. 2015 21:02

↑ Mauz: Jeden směr mi připadne snadný. Když má matice A hodnost jedna, tak řádky matice A jsou vždy násobek nějakého nenulového vektoru, který generuje bázi lin. prostoru řádku matice A. i-tý řádek matice 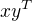$xy^{T}$ je pak 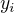$y_{i}$ násobek vektoru $x$ .

Matematické Fórum

#1 16. 12. 2015 18:55 — Editoval Mauz (16. 12. 2015 18:56)

Hodnost matice a součin aritmetických vektorů

#2 16. 12. 2015 21:02

Re: Hodnost matice a součin aritmetických vektorů

Zápatí