Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Posloupnosti funkcí - limita se suprémovou a L2 metrikou
#1 27. 12. 2015 18:13
- Katsushiro

- Místo: Rožnov pod Radhoštěm
- Příspěvky: 144
- Škola: VŠB TUO - FEI
- Pozice: student
- Reputace: 2
Posloupnosti funkcí - limita se suprémovou a L2 metrikou
Ahoj všichni!
Tak se snažím pochopit metrické prostory, ale sekl jsem se na následujícím příkladu:
Mám zadány následující posloupnosti funkcí na definičním oboru  :
:
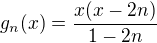
U obou mám zjistit, jestli je posloupnost Cauchyovská a jestli má limitu v prostoru:
1)  se supremovou metrikou
se supremovou metrikou
2)  s L2 metrikou
s L2 metrikou
Supremová metrika: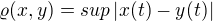
L2 metrika: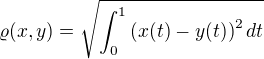

Moje řešení:
Pokusil jsem se načrtnout první funkce posloupností:
Funkce tady vždy pokračuje dál po ose X, tedy  .
.
Jinak tedy jde posloupnost nejspíš k funkci  .
.
Tady se posloupnost postupně blíží k funkci 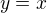 .
.
A tady jsem zatím skončil, protože si vůbec nejsem jistý, jak pracovat s posloupností funkcí. Vím, že prostor  se supremovou metrikou je úplný, a tentýž prostor s L2 metrikou není úplný. V prvním případě tedy bude stačit, když je posloupnost Cauchyovská a bude konvergentní, ve druhém vůbec nevím.
se supremovou metrikou je úplný, a tentýž prostor s L2 metrikou není úplný. V prvním případě tedy bude stačit, když je posloupnost Cauchyovská a bude konvergentní, ve druhém vůbec nevím.
Ohledně určení toho, jestli je posloupnost Cauchyovská, mě ještě napadá, že bych porovnal funkční hodnoty v libovolném bodě. S ohledem na to by obě posloupnosti byly Cauchyovské a tedy konvergentní v prvním případě.
Doufám, že jsem problém popsal jakž-takž jasně. Pokud byste věděli, prosím, poraďte, jak dál, v tomhle se nějak moc nechytám.
Moc díky za všechny rady,
Katsu
Offline
#2 27. 12. 2015 18:41 — Editoval Bati (27. 12. 2015 20:28)
Re: Posloupnosti funkcí - limita se suprémovou a L2 metrikou
Ahoj ↑ Katsushiro:.
Než začneš něco počítat, je dobrý se zamyslet, v jakém vztahu ty konvergence jsou. Prostor C[0,1] s L2 metrikou není úplný také kvůli tomu, že případná limitní funkce je určena až na množinu míry nula, tj. není jednoznačná. Po ztotožnění funkcí, které se rovnají skoro všude je L2(0,1) úplný. Konvergence v suprémové metrice znamená stejnomernou konvergenci a ta implikuje konvergenci ve všech Lp prostorech díky vnoření.
Offline
#3 27. 12. 2015 20:04
- Katsushiro

- Místo: Rožnov pod Radhoštěm
- Příspěvky: 144
- Škola: VŠB TUO - FEI
- Pozice: student
- Reputace: 2
Re: Posloupnosti funkcí - limita se suprémovou a L2 metrikou
↑ Bati:
Takže pokud to chápu...
1) Obě se k něčemu blíží, proto jsou Cauchyovské
2) Obě konvergují v supremové metrice, tj. limita 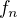 je
je  a limita
a limita 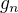 je
je 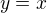 .
.
Omlouvám se, ale to s L2 metrikou jsem nepochopil. Mohl bys trochu rozvést to "určena až na množinu míry 0"? A co myslíš "ztotožněním funkcí"?
Moc díky a sorry za další dotazy, ale jsem v tomhle fakt začátečník :-)
Offline
#4 27. 12. 2015 21:05
Re: Posloupnosti funkcí - limita se suprémovou a L2 metrikou
↑ Katsushiro:
Zatím jsem to psal jen tak obecně, aby sis uvědomil vztahy mezi těmi prostory. Na Lp prostorech se zavádí ekvivalence, aby to vůbec byl normovaný lineární prostor. Tobě sice stačí, aby to byl metrický prostor, ale bez této ekvivalence nemůžeš požadovat jednoznačnost případných limit. Třídy těch ekvivalencí tvoří funkce, které se rovnají skoro všude, o tom už jsi musel slyšet. Ono to je ale nakonec jedno, protože případná limita v L2 metrice už nemusí být spojitá funkce.
K tvému příkladu: Na základě tvého náčrtku bych dokazoval, že fn není Cauchyovská, a tedy nekonverguje v sup. metrice (k nule), ale konverguje v L2 metrice k nule (k třídě funkcí, která obsahuje nulovou funkci a funkce, které jsou nula skoro všude). gn už by měla konvergovat stejnoměrně.
Offline
#5 27. 12. 2015 21:30
- Katsushiro

- Místo: Rožnov pod Radhoštěm
- Příspěvky: 144
- Škola: VŠB TUO - FEI
- Pozice: student
- Reputace: 2
Re: Posloupnosti funkcí - limita se suprémovou a L2 metrikou
↑ Bati:
Tak to asi chápu blbě...
Proč není 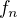 Cauchyovská? Měl jsem za to, že se k sobě jednotlivé prvky posloupnosti, resp. funkce víc a víc blíží...
Cauchyovská? Měl jsem za to, že se k sobě jednotlivé prvky posloupnosti, resp. funkce víc a víc blíží...
Offline
#6 27. 12. 2015 22:32 — Editoval Bati (27. 12. 2015 22:46)
Re: Posloupnosti funkcí - limita se suprémovou a L2 metrikou
↑ Katsushiro:
U nuly ne. Ať vezmeš libovolně velký n, tak vždycky najdu m>n tak velký, že 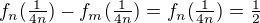 .
.
Pokud víš, že prostor C[0,1] je úplný vzhledem k sup. metrice, můžeš argumentovat i takto: Posloupnost 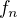 konverguje bodově k nulové funkci na (0,1] a k jedničce v bodě nula. To ale není spojitá funkce, tudíž není možné, aby
konverguje bodově k nulové funkci na (0,1] a k jedničce v bodě nula. To ale není spojitá funkce, tudíž není možné, aby 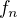 konvergovala stejnoměrně (jednoduché tvrzení z analýzy). Tzn., že
konvergovala stejnoměrně (jednoduché tvrzení z analýzy). Tzn., že 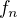 nekonverguje v prostoru C[0,1] se supremovou metrikou, který je ovšem úplný, tudíž
nekonverguje v prostoru C[0,1] se supremovou metrikou, který je ovšem úplný, tudíž 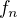 nemůže být Cauchyovská.
nemůže být Cauchyovská.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Posloupnosti funkcí - limita se suprémovou a L2 metrikou