Matematické Fórum

zdenos · 15. 01. 2016 16:30

Dobrý den,

pomuze mi někdo s následujícím?

potřebujeme spočítat nevyužitelný objem kotle, když je lomený /spádovaný 1% ke středu.

Je to to nad červenou ryskou. U víka naplněno po horní okraj nádoby, ale zvednuté okraje mají nevyužitou vzduchovou kapsu. Délka i průměr válce jsou známy ( 2650 /14200 ) Zaoblení čel zanedbáme. Takže nemusí to být zcela přesné

obrazek vagonu:
//forum.matweb.cz/upload3/img/2016-01/71758_va.JPG

Dekuju

Sergejevicz · 15. 01. 2016 17:59

Jestliže to nemusí být úplně přesně, tak to budu chápat tak, že délka jedné kapsy je půlka délky válce, i když lomení válce dělá to, že jeho délka nahoře je menší než dole...

Označení:
$h=\text{polovina délky (správně geometricky výšky) válce}$
$R=\text{poloměr válce (myšlen poloměr vnitřního prostoru vyplnitelného tekutinou nebo plynem)}$
$s=\text{spád (je třeba ho přepočítat na jednotky, tj. ze zadání to bude }0,01\text{)}$

K tomu mám poznámku, že asi zadaná čísla jsou prohozená :-). Pozor, do mého náznaku, viz dále obrázek, je třeba správně dosadit uvažované veličiny, zejména zdůrazňuju POLOměr, viz označení výše.

:-)

//forum.matweb.cz/upload3/img/2016-01/77095_Cisterna.jpg

Sergejevicz · 15. 01. 2016 18:01

Jinak $p=\tan\beta$ .

Sergejevicz · 15. 01. 2016 18:10

Jiná možnost: nakreslit si to počítané těleso v nějakém CAD-softwaru a objem nechat spočítat ten CAD-software :-). Například software Salome je zdarma.

Sergejevicz · 15. 01. 2016 18:27

A omlouvám se za mušince a škrtance :-).

misaH · 15. 01. 2016 19:14

↑ Sergejevicz:

:-)

zdenos · 16. 01. 2016 13:22

Dekuji za blizsi vysvetleni, ale je mozne sem dat primo konkretni vypocet s vysledkem?

jelena · 16. 01. 2016 15:37

Zdravím,

↑ zdenos: pro konkrétní výpočet je vhodné doplnit, zda jde o dotaz z praxe a z jakého oboru cca je, případně jak bude řešení využito - je to zajímavé a téma přesunu do sekce "Úloh pro praxi". Jinak, pokud jde o úlohu školní, potom je třeba postupovat dle pravidel - viz pravidla (bod 3). Upřesni, prosím.

zdenos · 16. 01. 2016 15:48

Zdravim,

je to uloha z praxe. Obor logistika. vypocet je dulezity pro vypocet stupne plneni jednotlivych vagonu, jelikoz vyrobce udava cely objem vagonu tzn. i to co je nadhladinou a nelze plnit.

Ano je mozne vagon naplnit a tak zjistit kolik se do nej vejde, ale pro me je dulezite kolik by se veslo do vzduchovych kapsi, ktere vznikaji diky sklonu vagonu do jeho stredu.

Dekuji

jelena · 16. 01. 2016 17:50

↑ zdenos:

děkuji za upřesnění, přesunu do úloh pro praxi. Pro výpočet integrálu můžeš hodnoty vložit sem Odkaz.
Před časem jsme diskutovali obdobný problém - kolega Eratosthenes navrhnul řešení, které lze využit i se základní zkušenosti s integrováním (co se bere na SŠ), musel bys ještě upravit rozměry, jelikož ve Tvém případě řez nepůjde přesně do poloviny válce, ale dle zadání, že sklon je 1 %. Jinak pro vagony není omezení (nevyužití celého objemu) jen v konstrukci (že je spadován), ale také se předpokládá teplotní roztažnost materiálů, tvorba výparů apod. a % nezaplnění by mělo být dáno příslušným standardem.

Sergejevicz · 16. 01. 2016 22:48

zdenos napsal(a):
Dekuji za blizsi vysvetleni, ale je mozne sem dat primo konkretni vypocet s vysledkem?

Vždyť jsem napsal začátek výpočtu. Co jsem nenapsal, je to, jak konkrétně se integrál spočítá, a také to, co vyjde, když se dosadí konkrétní hodnoty. To by se měl zadávající snažit dopočítat sám, jde o to prostě provést integrování, já jsem dodatl zformulování integrálu. Nebo zadavatel neumí integrovat a dosadit konkrétní hodnoty? :-)

Sergejevicz · 16. 01. 2016 22:52

jelena napsal(a):
↑ zdenos:
...a % nezaplnění by mělo být dáno příslušným standardem.

Také je potřeba dát pozor na to, aby nezaplnění nebylo moc velké, protože pak se kapalina může snadno rozkmitat a myslím, že by mohlo dojít i k vykolejení. Kdyžtak mě opravte.

Vlak se sice pohybuje s menšími setrvačnými účinky než např. nákladní automobil, ale vlakové tratě taky nemají ideální geometrii a myslím, že i na nich může k rozkmitání dojít.

zdenos · 17. 01. 2016 08:00

↑ Sergejevicz:
Bohužel integrovani mi nic.moc neříká. Opravdu bych potřeboval ukázat postup výpočtu.

Děkuju

misaH · 17. 01. 2016 10:11

↑ zdenos:

:-)

A načo ti to bude, keď ti to nič nehovorí?

zdenos · 17. 01. 2016 10:15

↑ misaH:

Jde mi o postup a výsledek. Ne o to jak se počítají integrály. Ty vagóny jsou pořád stejne, takže to vyuziji 1x a bude to platne porad

jelena · 17. 01. 2016 12:36

Zdravím,

sekce dotazů pro praxi byla myšlena, že autor dotazu nemusí mít dostatečný matematický aparát, vyřešení potřebuje pro praktické účely a celkové odvození ani tak moc ne (je to spíš záležitost diskuse kolegů, kdo se do tématu zapojí). U této otázky odvozený vzorec lze najít ve strojírenských tabulkách jako "Část rotačního válce" (tzn. válcové kopyto) - vidím to v knize "Strojirenská příručka. Svazek 1, SNTL, 1992". Online český text jsem nenašla, ale tento ruský je přehledný - viz "Цилиндрическое копыто" - Náhled, je nutné doplnit výpočet úhlu $\varphi$ v návaznosti na zadaný sklon.

↑ zdenos: Stačí Tobě takový vzorec, nebo potřebuješ celé odvození pomocí integrálu (buď trojného, nebo tak, jak je u kolegy v odkazu, co jsem dávala). Pokud integrování neovládáš (nebo už jsi vyšel ze cviku), tak vzorec bys lépe uplatnil. Podle posledního příspěvku bych řekla, že postupem postačí technika v odkazu, co jsem dávala, nebo kolegy ↑ Sergejevicz:, ale sama se ještě v označeních kolegy neorientuji :-) Trojný integrál jsem odvozovala v předchozím tématu, teď bych ho musela upravit na jiný sklon a odvodit obecně, ale zatím bych nenarušovala odvození kolegy, stejně to teď časově bych nestihla.

↑ Sergejevicz: pevně věřím, že ČSN na kolejová vozidla všechno vyřeší za mne :-).

zdenos · 17. 01. 2016 14:09

↑ jelena:

Budu mluvit narovinu. Matika neni muj obor. Potreboval bych ukazat primo konkretni postup a vysledek.

Dekuju

jelena · 17. 01. 2016 14:56

↑ zdenos:

dobře - postup odvození je např. zde. Pro Tvé výpočty se budu držet vzorce, který najdeš ve Strojírenské příručce a který je v ruském odkazu. Objem jedné kapsy (pro polovinu vagonu) vypočteme dle vzorce
$V=\frac{h}{3b}$a\(3R^2-a^2$-3R^2$R-b$\cdot \varphi\)$ ,
dle označení na obrázku a Tvého vagonu: $R$ -poloměr vagonu, $h$ -polovina délky vagonu, $a, b, \varphi$ - viz obrázek (pomocné rozměry pro výpočet). Pokud je zadán sklon $p$ v procentech, potom $b=\frac{hp}{100}$ , $\cos \varphi=\frac{R-b}{R}$ , odsud hodnota $\varphi$ a dosadit do $a=R\sin \varphi$ .
To všechno použit do vzorce pro objem kapsy.

Zkus to zadat např. do EXCEL a vypočítat pro pár skutečných hodnot (až bude více času, můžeme podiskutovat, kterým tělesem lze nahradit to, co počítáme, aby šlo použit některý online kalkulátor pro částečně plněné válce). Dej, prosím vědět, jak vychází (zda nemám nějaký překlep v přepisu nebo v odvození). Děkuji.

zdenos · 17. 01. 2016 19:04

↑ jelena:

Ahoj

pro kontrolu:

R=1325
h=7100
a= ? (podle obrazku mi to prijde jako polomer)
b=2650 prumer vagonu

jeste se zeptam. Procento sklonu zadavam jako 1 nebo to musim prevadet? napr. 0,01 atd.

Je to hloupe, ale myslis, ze by slo z tvoji strany to primo nazorne dosadit CO, KAM, KDE patri.

Diky za pomoc

jelena · 18. 01. 2016 09:30

↑ zdenos:

a, b počítáme na konkrétní situaci, podle toho, jak je zadán sklon. Ještě se podívej na obrázky v odkazech. Vzorec pro použití sklonu mám tak, aby se dosazovalo v procentech (tedy 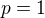$p=1$ ). Dosazujeme $b=\frac{hp}{100}=\frac{7100\cdot 1}{100}=71$ , $\cos \varphi=\frac{R-b}{R}=\frac{1325-71}{1325}=...$ odsud určuji úhel $\varphi$ a dosazuji do vzorce pro výpočet $a=R\sin \varphi$ (výpočet WA), budu používat $a=428$ .
Všechno dosazuji do vzorce pro
$V=\frac{h}{3b}$a\(3R^2-a^2$-3R^2$R-b$\cdot \varphi\)=\frac{7100}{3\cdot 71}$428\(3\cdot 1325^2-428^2$-3\cdot 1325^2$1325-71$\cdot 0.3288\)$

objem kapsy nad polovinou vagonu: (výpočet WA).

Pro velmi hrubý odhad počítám objem kvádru nad obdélníkem opsaným kruhové úseči, která mi vznikne v bočním čele vagonu, rozměry obdélníků jsou $a=428$ , $b=71$ . Výška kvádru je $h=7100$ . Jelikož "sklonem podělím kvádr velmi hrubo na poloviny, vezmu polovinu takového kvádru - výsledek, což je slušný odhad. Podle mne takovým kvádrem můžeš odhadovat nezaplněnou část docela obstojně.

Pořád jsme počítali kapsu nad jednou polovinou vagonu. Je to tak dostatečně přehledné? Co s tím v konečném výsledku budeš dělat? Děkuji.

zdenos · 18. 01. 2016 11:09

↑ jelena:

Ahoj,

klobouk dolů.

Ještě mi rekni, výsledek pro 1 kapsu je ten druhy odkaz pod hlavnim vzorcem? nebo ten poslední odkaz dole - 215 754 800 mm3?

Je to pro overeni, jestli výrobce vagonu udava spravne udaje o objemu vagonu. Nekdy poslou objem celého vagonu i s tim co se neda plnit a nekdy zas jen s tim co se da plnit. Podle jejich cisel je volne místo(vzduchova kapsa) pro 1 vagon 400 l

Moc dekuju.

jelena · 18. 01. 2016 14:00

↑ zdenos:

také děkuji, výhodou je, že vzorec je hotový, není nutné odvozovat.

1. výsledek je 1,3*10^8 mm^3 a je pro jednu kapsu, pro celý vagon je 2,6*10^8 mm^3=260 litrů.
2. výsledek je hrubší odhad objemu pomocí poloviny kvádru, jak je popsáno, pro celý vagon je to 430 litrů.

Je to pro overeni, jestli výrobce vagonu udava spravne udaje o objemu vagonu. Nekdy poslou objem celého vagonu i s tim co se neda plnit a nekdy zas jen s tim co se da plnit. Podle jejich cisel je volne místo(vzduchova kapsa) pro 1 vagon 400 l

řekla bych, že to souhlasí.

Honzc · 23. 01. 2016 11:00

↑ jelena:
Zravím,
jestli se dobře dívám na obrázek cisterny, (osa, která je tam nakreslena není rovnoběžná s "kolejemi") pak tvůj výpočet není úplně dobře.
Rozměry budu vujadřovat v metrech.
$R=1.325+0.071=1.396$
Dále vychází $a=0.439535$ a $\varphi =0.320302$

Správný výpočet pak je Tady

Tento výpočet je dělán pro válec, což samozřejmě u dané csterny neplatí ( polovina cisterny je totiž obecný (nerotační) komolý jehlan)
Proto přesný výsledek bude o něco menší, než vychází výpočtem.
Ověřil jsem to namodelováním a vychází $V=0.1149..m^{3}$

jelena · 23. 01. 2016 14:02

↑ Honzc:

Zdravím a děkuji,

zde je potíž tohoto rázu - kolega v úvodním příspěvku problém nějak naformuloval ↑ příspěvek 1:, potom ještě doplňuje, že úloha z praxe, ověření údajů výrobce atd. Navíc je vidět, že s matematickým aparátem trochu bojuje. Řekneme si proto, že výpočet si usnadníme nalezením hotového vzorce v tabulkách + pokusíme se provést nějaký rozumný odhad např. pomocí SŠ postupů (to by technik v běžné praxi měl zvládnout) - viz také postup pro SŠ kolega Eratosthenes.

Výrobce udává 400 litrů, můj výpočet pro 2 kapsy dává 2*130=260 (litrů), Tvůj výpočet pro 2 kapsy dává 2*115=230 (litrů). Můj hrubý odhad (pomocí poloviny kvádru) dává 430 litrů.

Pokud objem cisterny cca 63210 litrů, kapsa činí nějakých 0,5% od objemu. řekni mi jako technik, zda bys se věnoval nějakému přesnějšímu výpočtu, než slušnému odhadu.

A navíc - pokud dojde k řízení ohledně dodávek, tak jediným platným podkladem bude údaj ze stanoveného měřidla (zde nejspíš hmotnostní nebo objemové). Kolega ještě něco upřesňoval v PM, na což jsem mu napsala mimo jiné toto:

Údaje od výrobce musí být spíš orientační - výpočet je postaven na tom, že považujeme všechny rozměry za ideální (bez tolerance), že vagon stoji přesně vodorovně atd. Pokud jsme řádově vyšli jako výrobce - naších přesných 260 litrů, nebo i cca 300 nebo 500 l by bylo pořád ve shodě. V obchodním styku stejně byste měli využívat takové měřidlo, které jednoznačně prokáže skutečný objem (nebo hmotnost) za stanovených podmínek, ve stanovené toleranci a při platném ověření měřidla. Viz předpisy okolo metrologie.

Pokud by šlo o nedostatečné využití dopravního prostředku, tak povinný nevyužitý objem (tipuji) bude daleko větší, než 0,5%. Tedy pro praktické účely bychom vyvážili přesnost výpočtu a čas vyčleněný na takový výpočet.

Co je nemilé :-) Hned v sousedním tématu vidím stejně formulovaný problém a opět na válci. Tak mám to brát tak, že autor tématu podává zavádějící informaci o účelu výpočtu? Počkáme, zda se neozve a popřípadě model výpočtu upřesníme - nejlépe přesně podle předmětu a zadání (pokud je to skutečně zadání na VŠ). Na druhou stranu - pokud je to na VŠ, tak si svůj (náš) výpočet už musí obhajovat sám, když mu stačil.

Sněží u vás? Děkuji a zdravím také bratra :-).

Matematické Fórum

#1 15. 01. 2016 16:30

Integral - vypocet nevyuzitelneho mista vagonu

#2 15. 01. 2016 17:59

Re: Integral - vypocet nevyuzitelneho mista vagonu

#3 15. 01. 2016 18:01

Re: Integral - vypocet nevyuzitelneho mista vagonu

#4 15. 01. 2016 18:10

Re: Integral - vypocet nevyuzitelneho mista vagonu

#5 15. 01. 2016 18:27

Re: Integral - vypocet nevyuzitelneho mista vagonu

#6 15. 01. 2016 19:14

Re: Integral - vypocet nevyuzitelneho mista vagonu

#7 16. 01. 2016 13:22

Re: Integral - vypocet nevyuzitelneho mista vagonu

#8 16. 01. 2016 15:37

Re: Integral - vypocet nevyuzitelneho mista vagonu

#9 16. 01. 2016 15:48

Re: Integral - vypocet nevyuzitelneho mista vagonu

#10 16. 01. 2016 17:50

Re: Integral - vypocet nevyuzitelneho mista vagonu

#11 16. 01. 2016 22:48

Re: Integral - vypocet nevyuzitelneho mista vagonu

zdenos napsal(a):

#12 16. 01. 2016 22:52

Re: Integral - vypocet nevyuzitelneho mista vagonu

jelena napsal(a):

#13 17. 01. 2016 08:00

Re: Integral - vypocet nevyuzitelneho mista vagonu

#14 17. 01. 2016 10:11

Re: Integral - vypocet nevyuzitelneho mista vagonu

#15 17. 01. 2016 10:15

Re: Integral - vypocet nevyuzitelneho mista vagonu

#16 17. 01. 2016 12:36

Re: Integral - vypocet nevyuzitelneho mista vagonu

#17 17. 01. 2016 14:09

Re: Integral - vypocet nevyuzitelneho mista vagonu

#18 17. 01. 2016 14:56

Re: Integral - vypocet nevyuzitelneho mista vagonu

#19 17. 01. 2016 17:18 Příspěvek uživatele zdenos byl skryt uživatelem zdenos.

#20 17. 01. 2016 19:04

Re: Integral - vypocet nevyuzitelneho mista vagonu

#21 18. 01. 2016 09:30

Re: Integral - vypocet nevyuzitelneho mista vagonu

#22 18. 01. 2016 11:09

Re: Integral - vypocet nevyuzitelneho mista vagonu

#23 18. 01. 2016 14:00

Re: Integral - vypocet nevyuzitelneho mista vagonu

#24 23. 01. 2016 11:00

Re: Integral - vypocet nevyuzitelneho mista vagonu

#25 23. 01. 2016 14:02

Re: Integral - vypocet nevyuzitelneho mista vagonu

Zápatí