Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 17. 01. 2016 11:52
Důkaz
Ahoj, potřebuji pomoc s důkazem tohoto příkladu:
Nechť x je reálné číslo takové, že x + 1/x je celé. Dokažte, že potom je pro každé  n číslo
n číslo  celé.
celé.
Osobně bych to řešila matematickou indukcí, pro n = 1 je to jasné, ale pro n + 1 už nevím co s tím.
Předem děkuji za rady
Offline
#2 17. 01. 2016 22:47
Re: Důkaz
Jen tak pro inspiraci
Ukážu, že výraz  jde zapsat ve tvaru
jde zapsat ve tvaru  a
a 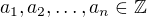 pro každé kladné celé
pro každé kladné celé  . Pro
. Pro 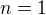 je tvrzení zřejmé, pro
je tvrzení zřejmé, pro 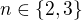 máš příklady výše.
máš příklady výše.
Předpokládejme, že pro vhodné celé koeficienty 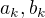 platí
platí  a
a  . Vynásobme první rovnost výrazem
. Vynásobme první rovnost výrazem 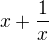 , tj.
, tj.  , po úpravě
, po úpravě  , kde klademe
, kde klademe  , čímž je naše tvrzení dokázáno.
, čímž je naše tvrzení dokázáno.
Teď otázka pro tebe, jak z toho tvrzení plyne, že  je celé číslo? :)
je celé číslo? :)
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline

