Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 01. 2016 16:24 — Editoval Tomas5 (28. 01. 2016 17:21)
řada s kombinačními čísly
Dobrý den, narazil jsem na úlohu, se kterou si nevím rady, přestože je k němu nápověda.
Spočtěte 
Nápověda (chyták - nemusí vést k řešení) :
Je známý výsledek - , ale nevím jakým postupem se k němu dostat. Děkuji za odpovědi.
Offline
#2 28. 01. 2016 18:51
Re: řada s kombinačními čísly
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#4 28. 01. 2016 20:12
Re: řada s kombinačními čísly
↑ Tomas5:
Teď bych zkusil z kombinačního čísla 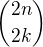 "nějak vytvořit" kombinační číslo
"nějak vytvořit" kombinační číslo 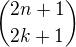
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#6 28. 01. 2016 21:28
Re: řada s kombinačními čísly
↑ Tomas5:
Tak jednoduše to nejde, se sumou takhle pracovat nemůžeš, tj.
Pomůže Ti, když najdeš konstanty  a
a  takové, že
takové, že
Sumu vlevo pak rozepiš na dvě sumy: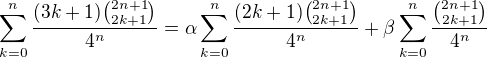
a budeš téměř na konci.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#8 28. 01. 2016 21:59
Re: řada s kombinačními čísly
↑ Tomas5:
Opět stejná chyba
První suma se upraví takto (a na konci se použije nápověda):
Druhá suma je rovna 1 (bez sumačního znaku), tj.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline

 .
.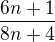
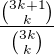
 , a co dál, prosím?
, a co dál, prosím?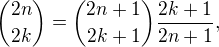 pak bude
pak bude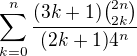
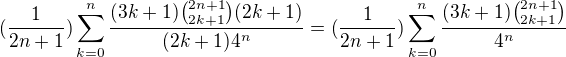 a protože je
a protože je 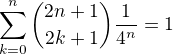
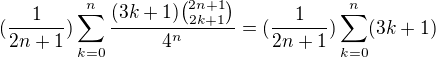 . Je to dobře? A co dál?
. Je to dobře? A co dál?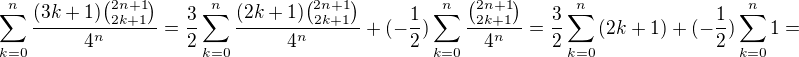 , tedy
, tedy 
 podle tvého návodu
podle tvého návodu a
a