Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Dělení mnohočlenu mnohočlenem (reciproká rovnice) (TOTO TÉMA JE VYŘEŠENÉ)
#1 23. 05. 2009 21:59
- docasne123
- Příspěvky: 56
- Reputace: 0
Dělení mnohočlenu mnohočlenem (reciproká rovnice)
Ahoj,
nějak mi nevychází dělení .
.
Pozn. má se jednat o (záporně) reciprokou rovnici. Chci se zeptat jestli jdu vůbec správným směrem. Kladně reciproké rovnice (kde jsou exponenty sestupně postupně) mi jdou, ale tady se nějak nemůžu dostat ke správnému výsledku. Ten mnohočlen má být i zadání oné rovnice (pro jistotu to napíšu samostatně znovu). Chci se zeptat jestli vůbec tím dělením začínám dobře, nebo jestli dělám nějakou blbost.
Díky
Offline
#3 23. 05. 2009 23:32
- docasne123
- Příspěvky: 56
- Reputace: 0
Re: Dělení mnohočlenu mnohočlenem (reciproká rovnice)
Měl jsem pocit, že jo ;-). Už jsem to vydělil, furt jsem tam dělal stenou chybu (opačně znaménko), a tak mi tam neustále vycházel zbytek.
Dostal jsem se na
Je to lichý stupěň I. druhu reciproké rovnice, tak jsem to znovu vydělil, teď ale výrazem (x + 1)
Výsledek je (věřím, že dobrý):
Mohl by mi někdo poradit jak dál ?
(Zkoušel jsem vydělit  nebo
nebo 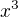 , pak ale nevím co s tím.)
, pak ale nevím co s tím.)
Offline
#5 23. 05. 2009 23:57
- docasne123
- Příspěvky: 56
- Reputace: 0
Re: Dělení mnohočlenu mnohočlenem (reciproká rovnice)
Díky moc pustím se zatím s počítáním dál. Mohl bych ale ještě poprosit o vysvětlení/rozepsání co jsi udělal mezi 2. a 3. krokem že ti vzniklo to co ti vzniklo. Chápu že do druhého obrázku jsi vytkl ze členů čísla 4 a 13. (Základní operace s mnohočleny jsem si bohužel nidky neosvojil).
Offline
#6 24. 05. 2009 00:06
Re: Dělení mnohočlenu mnohočlenem (reciproká rovnice)
:) jasný,hele nejdřív vytkneš čtyřku z členů,kde je čtyřka,potom jsem ztěch zbylých vytknul minus třináct,ale vznikl tam patvar,proto sem vytknul -13x na druhou....Potom jsem vytknul,co měli ty závorký společné a vzniklo stoho tohle....když by nevyšli kořeny,tak to skontroluj a nebudeš-li si vědět rady,možná to bude má chyba,já to kontroloval,mělo by to být dobře,ale je přeci jenom půlnoc a já nemám ve zvyku o půlnoci počítat rovnice sedmého stupně :D
Volané číslo je imaginární. Otočte prosím telefon o 90 stupňů a zkuste to znovu.
Offline
#7 24. 05. 2009 00:14
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Dělení mnohočlenu mnohočlenem (reciproká rovnice)
↑ docasne123:
Zdravím, myslím, že kolega ↑ Alivendes: má velmi netradiční postup - asi to sam vysvětli.
Nekontrolovala jsem tvoje jednotlivé kroky, ale pokud je toto OK:  , pak máš dělit
, pak máš dělit 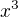 .
.
V dalším kroku vytkneš z 1. a 4. členu 4 (v závorce bude  ) a z 2. a 3. clenu vytknes (-13) (v závorce
) a z 2. a 3. clenu vytknes (-13) (v závorce 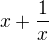 )
)
substituce 
Je to trochu hopem, snad nemám nějaký úlet.
OK?
Offline
#9 24. 05. 2009 00:24 — Editoval docasne123 (24. 05. 2009 00:29)
- docasne123
- Příspěvky: 56
- Reputace: 0
Re: Dělení mnohočlenu mnohočlenem (reciproká rovnice)
To[Alivendex]
Doufám, že neponocuješ jenom kvůli mně. Díky za vysvětlení, myslím, že jsem to pochopil, a myslím že to máš dobře, jenže...
z té 1. závorky jsem vydělil (x+1) zbylo  => kořeny
=> kořeny  .Což je ok (btw. správné kořeny mají být
.Což je ok (btw. správné kořeny mají být  .Dokonce jsem i na internetu našel nějaký hledač kořenů rovnic, který potvrdil, že to tak má být (není špatné zadání).
.Dokonce jsem i na internetu našel nějaký hledač kořenů rovnic, který potvrdil, že to tak má být (není špatné zadání).
Ale z té 2. závorky (edit: převedl jsem na kvadratickou rovnici) mi vychází hrozné čísla.
Edit: a navíc z kvadtarické nevydoluju 4 kořeny vím, že je možné kořeny "ztratit" nebo si naopak jich víc "vytvořit" nevíš ve které fázi jsem je "ztratil" já a jak je můžu dopočítat ?
To[Jelena]:Nehci se hádat (navíc v tuhle noční hodinu) když vydělím 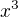 nevzniknu spíše
nevzniknu spíše  kde sice najdu ten člen
kde sice najdu ten člen 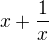 ale už ne
ale už ne  .
.
Dotaz (navíc): torchu předbíhám, ale ... vím jak mám substituovat až do  (našel jsem to na netu), nechápu jak to ale odvodili, a jak by se substituovaly vyšší exponenty jako
(našel jsem to na netu), nechápu jak to ale odvodili, a jak by se substituovaly vyšší exponenty jako  atd.
atd.
Ad. Omlouvám se za překlepy (Edit: a jestli vás matematicky urážím a píšu už bludy).
Offline
#10 24. 05. 2009 00:31
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Dělení mnohočlenu mnohočlenem (reciproká rovnice)
↑ docasne123:
Vše OK, ale myslím, že už je dost pozdní hodina, tak bychom to mohli nechat na zitra. Souhlas?
Offline
#11 24. 05. 2009 00:34
- docasne123
- Příspěvky: 56
- Reputace: 0
Re: Dělení mnohočlenu mnohočlenem (reciproká rovnice)
↑ jelena:
jo, omlouvám se. Já ty exponenty dělil místo odčítal, jejej.
Offline
#13 24. 05. 2009 00:38
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Dělení mnohočlenu mnohočlenem (reciproká rovnice)
↑ Alivendes:
Dobrou :-)
↑ docasne123:
Já bych poprosila o další postup kolegu halogana, pokud má čas a naladu, děkuji :-)
jinak opravdu až zítra. OK?
Offline
#14 24. 05. 2009 00:46
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Dělení mnohočlenu mnohočlenem (reciproká rovnice)
↑ jelena:
No hele nevím. Reciproké (nebo polynomické obecně) rovnice jsem již přesně rok nedělal a pamatuji si akorát Hornerovo schéma a substituci y = x + 1/x
Nějak nechápu, jak postupoval kolega ↑ Alivendes:, tak jsem si řekl, že to vyřeším po svém.
Z původního
Jsem povytýkal co šlo a tím pádem "vyhodil" x+1. Pak se ale dostávám do úzkých. Resp. mohu dělit  , ale neznám nějaké univerzální řešení. A to dělení provádím právě podle Hornera.
, ale neznám nějaké univerzální řešení. A to dělení provádím právě podle Hornera.
Offline
#15 24. 05. 2009 00:48
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Dělení mnohočlenu mnohočlenem (reciproká rovnice)
Postup urychlí, když si všimneme, že jsou všechny mocniny sudé. V rovnici
uděláme substituce  , máme
, máme  , po vydělení y-1
, po vydělení y-1 , po vydělení y+1
, po vydělení y+1
Vyřešíme kvadratickou rovnici, vyjde y=4 a y=1/4. Máme tedy 4 různé možnosti pro y, z nich 8 možností pro x.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#16 24. 05. 2009 01:29
- docasne123
- Příspěvky: 56
- Reputace: 0
Re: Dělení mnohočlenu mnohočlenem (reciproká rovnice)
Děkuji za prosté řešení od Kondry (já si předtím lámal hlavu jak to mám zjednodušit, když tam nemám všechny členy a přitom stačila "jenom" substituce). Kořeny tedy vyjdou, kdyby se to hodilo i někomu jinému.



Můžu se zepta jak bych se k té komplexní jednotce dostal přes ten druhý postup ? Při 1. dělením mám kořen  po druhém dělení
po druhém dělení  , pak mám substituci kde
, pak mám substituci kde  . Nevím jak bych to nalezení kořenů
. Nevím jak bych to nalezení kořenů  zdůvodnil zde.
zdůvodnil zde.
Opravdu děkuji všem za pomoc a ochotu.
Pozn. Omlouvám se, že jsem lhal, ale nemohl jsem to vydržet.
Offline
#17 24. 05. 2009 01:38
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Dělení mnohočlenu mnohočlenem (reciproká rovnice)
↑ docasne123:
Někde výše jsi psal, že ti zbylo (x^2 + 1) = 0. A tam je kořenem +-i.
Případně u řešení ↑ Kondr: ti po dosazení ze substituce vyjde také x^2 + 1 = 0
---
Jinak z formálního hlediska ti nemůžu odkývat zejména poslední řádek:
Když už, tak něco ve smyslu
(i když nevím, jak mohu vkládat absolutní hodnotu kolem množiny dvou prvků).
Spíš mi šlo o tu konstrukci  , protože to po vyčíslení vyjde
, protože to po vyčíslení vyjde  , což není to samé, jako
, což není to samé, jako 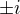
Offline
#18 24. 05. 2009 01:46
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Dělení mnohočlenu mnohočlenem (reciproká rovnice)
↑ halogan:
Zápis  má tu chybu, že
má tu chybu, že  a ne
a ne  .
.
šlo by to snad "spravit" takto:
ale osobně bych radši přechod od y k x popsal slovně ...
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#20 24. 05. 2009 11:51
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Dělení mnohočlenu mnohočlenem (reciproká rovnice)
Zdravím vás,
jiz tradiční poděkování kolegovi Kondroví za uvedení k rozumnému stavu a omluva za moji nedostatecnou duslednost.
Ano, měla jsem projit celé zadání a postup od začátku, ale reagovala jsem pouze na návrh ↑ Alivendes:, na dotaz ↑ docasne123: a na název tématu.
Naštěstí jsem žádné nepovolené kroky neprováděla. A pokud někoho jen vseobecne zajimá substituce používána v těchto typech reciprokých rovnic, tak to je tak: levou a pravou umocnime
levou a pravou umocnime
_____________________________



_______________________________
potrebujeme na 3. mocninu:




_______________________________
vyssi rozvoje podle binomicke vety nebo mozna by slo odvodit indukci, nezkousela jsem.
Offline
#21 24. 05. 2009 18:23
- docasne123
- Příspěvky: 56
- Reputace: 0
Re: Dělení mnohočlenu mnohočlenem (reciproká rovnice)
Ten rozklad vypadá taky zajímavě. Byl by někdo tak ochotný a vysvětlil by mi slovně co udělala (jak postupovala) v předposledním řádku s poslední závorkou
že z toho dostala
ad. ta komplexní jednotka. Máš pravdu místo
třeba tohle
Ještě jednou děkuji všem za pomoc.
Díky za to odvozování odvozením, tu binomickou větu na to zkusím (indukci myslím ještě neznám).
Offline
#22 24. 05. 2009 20:51
Re: Dělení mnohočlenu mnohočlenem (reciproká rovnice)
zvolila jsem substituci za x^2=a, vyšly 4 kořeny: +2, -2, +1/2, -1/2, odtud tedy (x-2)(x+2)(x-1/2)(x+1/2) - poslední dvě závorky lze upravit na (2x-1)(2x+1)
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Dělení mnohočlenu mnohočlenem (reciproká rovnice) (TOTO TÉMA JE VYŘEŠENÉ)



