Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 07. 02. 2016 22:48
Re: Limitka
↑ Sherlock:
Záleži na tom, zda n je nebo není přirozené číslo. Pokud ano, pak limita existuje a vychází opravdu 1. Nicméně dokázat, že tomu tak je, není triviální. Standardní prostředky mat. analýzy na to bohužel nestačí. Je mi divné, jak se takový příklad dostal do sekce "Úvod do studia".
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#6 07. 02. 2016 23:11
Re: Limitka
↑ byk7:
Beru částečně zpět svůj postřeh, vyšetřoval jsem limitu s absolutní hodnotou funkce cos. Původní limita i v případě přirozených čísel samozřejmě neexistuje.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#7 07. 02. 2016 23:14
Re: Limitka
↑ Pavel:
Zdravím,
rád bych se poučil. Mohl bys, prosím, okomentovat řešení z tohoto odkazu?
Offline
#8 07. 02. 2016 23:14 — Editoval van Thomas (07. 02. 2016 23:23)
- van Thomas

- Příspěvky: 61
- Škola: FAV ZČU
- Reputace: 5
Re: Limitka
↑ Pritt:
Ahoj, hledal jsi takovou dvojici, nebo jsi chtěl dokázat, že to platí pro každou takovou dvojici? (Neplatí)
Offline
#9 07. 02. 2016 23:16
- van Thomas

- Příspěvky: 61
- Škola: FAV ZČU
- Reputace: 5
Re: Limitka
↑ Al1:
to je nějaká hovadina ;-)
Offline
#11 07. 02. 2016 23:18 — Editoval van Thomas (07. 02. 2016 23:19)
- van Thomas

- Příspěvky: 61
- Škola: FAV ZČU
- Reputace: 5
Re: Limitka
 samozřejmě není (obecně) definované
samozřejmě není (obecně) definované
Offline
#12 07. 02. 2016 23:19 — Editoval Pritt (07. 02. 2016 23:19)
Re: Limitka
↑ van Thomas:
hledal jsem jednu takovou dvojici, wolfram mě navedl k tomu, že ta limita, o které se tu spekuluje, je rovna 1. :-)
Tak jsem se chtěl přesvědčit.
Offline
#14 07. 02. 2016 23:21 — Editoval van Thomas (07. 02. 2016 23:22)
- van Thomas

- Příspěvky: 61
- Škola: FAV ZČU
- Reputace: 5
Re: Limitka
↑ Pritt:
A znáš nějakou typickou posloupnost typu  ? Slyšels o
? Slyšels o  ?
?
Offline
#16 07. 02. 2016 23:24
Re: Limitka
↑ van Thomas:
Není mi jasné, proč se ptáš.
Zadání je:
Najděte posloupnosti (an), (bn) tak, že lim an = 1, lim bn = +infty a zároveň lim an^bn neexistuje.
Offline
#17 07. 02. 2016 23:25 — Editoval van Thomas (07. 02. 2016 23:29)
- van Thomas

- Příspěvky: 61
- Škola: FAV ZČU
- Reputace: 5
Re: Limitka
↑ Pritt:
Že bys ji mohl zkusit zmodifikovat, aby limita neexistovala ;-)
Napadá tě něco?
Offline
#18 07. 02. 2016 23:32
Re: Limitka
↑ van Thomas:
Jedině něco s an = (-1)^(2*n), ještě snažím nějak zapracovat tu druhou
Offline
#19 07. 02. 2016 23:34
- van Thomas

- Příspěvky: 61
- Škola: FAV ZČU
- Reputace: 5
Re: Limitka
↑ Pritt:
Něco takového, jen  je pro
je pro 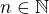 vždy
vždy  .
.
Offline
#20 07. 02. 2016 23:39
#21 07. 02. 2016 23:41
- van Thomas

- Příspěvky: 61
- Škola: FAV ZČU
- Reputace: 5
Re: Limitka
↑ Pritt:
To ne, 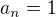 , takže
, takže  .
. 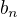 zbytečně komplikuješ, nech klidně
zbytečně komplikuješ, nech klidně  a promysli
a promysli  .
.
Offline
#23 08. 02. 2016 00:35 — Editoval Pritt (08. 02. 2016 00:36)
Re: Limitka
↑ van Thomas:


neexistuje.
Díky za rady van Thomas :-)
PS: Ještě by mě zajímalo, jak si to myslel s tím  .
.
Offline
#24 08. 02. 2016 00:45
- van Thomas

- Příspěvky: 61
- Škola: FAV ZČU
- Reputace: 5
Re: Limitka
↑ Pritt:
Ještě brzdi :)  nemá pro
nemá pro  moc smysl, rozhodně to nejde k
moc smysl, rozhodně to nejde k  . Zkusím tě víc navést na to, co jsem myslel já. Nech
. Zkusím tě víc navést na to, co jsem myslel já. Nech  . K čemu pak půjde
. K čemu pak půjde  pro
pro  a k čemu pro
a k čemu pro  ? A pak zkus ty dvě zkombinovat.
? A pak zkus ty dvě zkombinovat.
Offline








 ?
?






