Matematické Fórum

Katsushiro · 10. 02. 2016 16:58

Ahoj všichni!

Narazil jsem na následující důkazovou úlohu:

Dokažte, že lesy na grafu (podgrafy neorientovaného grafu, které neobsahují cyklus) splňují [jakožto množiny hran] axiomy I1,I2,I3; speciálně jde o I3, tedy o fakt, že když les F1 má více hran než F2, tak lze jednu hranu z F1, která není v F2, přidat k F2, aniž v něm vznikne cyklus.

Důkaz se evidentně týká matroidu a jeho axiomů. Chápu to tedy jako matroid M(E,I), kde E je množina všech hran grafu a I je množina všech nezávislých podmnožin E.

Axiomy pro množinu I jsou:
1) $\emptyset \subset E$
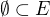
2) $\left(x \subseteq X\right) \wedge (X \in I) \Rightarrow (x \subseteq I)$
3) $(X,Y \in I) \wedge (||X|| < ||Y||) \Rightarrow \exists y \in (Y \setminus X): X \cup \{y\} \in I$

Vůbec ale netuším, jak dokázat, že to obecně platí.

Mohli byste mi, prosím, napovědět? :-)

Moc děkuji za všechny odpovědi,
Katsu

Matematické Fórum

#1 10. 02. 2016 16:58

Matroid - důkaz

Zápatí