Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 … 16 17 18 19 20 … 25
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Limitny maraton
#426 31. 07. 2019 15:17 — Editoval vanok (31. 07. 2019 19:32)
Re: Limitny maraton
Pozdravujem,
Toto cvicenie mozme aj takto riesit.
Najprv urcime mozne limity. ( to tu podrobne napisem).
A)
Ak  tak dana postupnost je nulova.
tak dana postupnost je nulova.
Tak predpokladajme, ze nie sme v takej situacii a vtedy rekurenciou mame, ze  . (*)
. (*)
Ak postupnost konverguje, tak jej limita  je taka, ze
je taka, ze 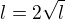 , cize
, cize 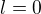 alebo
alebo  .
.
Ak by  pre kazde
pre kazde  , nasa postupnost by bola stupajuca a ohranicena cislom 1; a mala by tak limitu
, nasa postupnost by bola stupajuca a ohranicena cislom 1; a mala by tak limitu ![kopírovat do textarea $l\in [0;1]$](/mathtex/bf/bf19d26aea16b9912a4d50a6b0ef391b.gif) .
.
No vsak sme uz dokazali,ze to nie je mozne. Co nam tiez da, ze existuje  . Co da aj pre kazde
. Co da aj pre kazde 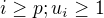 .
.
Tak je jasne, ze v situacii (*) jedina mozna limita je 4.
B)Navod na pokracovanie:
Na (dost elegantne riesenie) postupne polozme  , co da
, co da  ( pre kazde i ....)
( pre kazde i ....)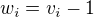 , a tu plati
, a tu plati 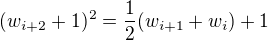 ( vdaka predoslej rovnosti).
( vdaka predoslej rovnosti).
co vyuzijeme...
Pochopitelne, ak treba, aj cast B) podrobne rozvediem.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#427 31. 07. 2019 16:50
Re: Limitny maraton
↑ vanok:
Kdyby byla posloupnost rostoucí, nebyla shora omezená a měla limitu nekonečno, nemohlo by však zároveň platit .
.
Musí být tedy shora omezena a mít tedy limitu rovnu čtyřem.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#428 31. 07. 2019 17:16
Re: Limitny maraton
Cau ↑ krakonoš:,
Len co budem mat trochu casu doplnim moje riesenie, cast B) ↑ vanok:
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#429 31. 07. 2019 19:31 — Editoval vanok (01. 08. 2019 21:38)
Re: Limitny maraton
↑ vanok:
Pokracovanie casti B) v ↑ vanok:.
Posledna rovnost da 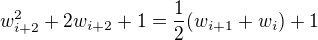 a tak po malej uprave
a tak po malej uprave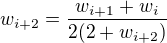
Pre kazde 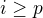 , je
, je 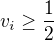 a tak
a tak 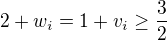 .
.
To nam da  .
.
Postupnost 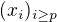 definovana rekurentne takto :
definovana rekurentne takto :  je klasicka rekurentna linearna radu 2, a preto
je klasicka rekurentna linearna radu 2, a preto  ( viete preco?).
( viete preco?).
A tak mame 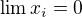
Tato kladna postupnost ohranicuje z hora postupnost
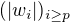 , co da
, co da 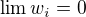
a tak aj
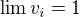 a tiez
a tiez 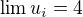 .
. Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#430 02. 08. 2019 15:55 — Editoval vanok (02. 08. 2019 15:59)
Re: Limitny maraton
Problem (88).
Nech  je realna funkcia klasy
je realna funkcia klasy  na
na  taka ze
taka ze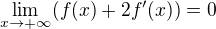 .
.
Urcite 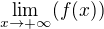 .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#431 03. 08. 2019 22:44
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Offline
#432 04. 08. 2019 09:07 — Editoval krakonoš (04. 08. 2019 09:17)
Re: Limitny maraton
↑ vanok:↑ check_drummer:
Ahoj,pozdravuji z Krkonoš.
Za předpokladu,že limita existuje by šlo možná uvažovat sporem,kdy máme dokázat,že pouze nulová limita vyhovuje.
Kdyby byla limita funkce f(x) kladná,aby měla funkce tuto limitu, musela by být od určitého x k této limitě klesající, nebo rostoucí,nebo by šla tato funkce shora i zdola omezit funkcemi,které jsou klesající a rostoucí a mají tutéž limitu - jako např u funkce sinx/x.
Celý problém lze podle mě redukovat na rostoucí či klesající funkci.
Kdyby byla tedy funkce f(x) klesající od určitého x a měla kladnou limitu L,s použitím trojúhelníkové nerovnosti na limitu,která má být rovna nule bychom dostali,že bychom museli umět dělat libovolně malé absolutni hodnotu(derivace funkce f(x) plus L/2),když je klesající,tak to není možné.
Podobně u rostoucí funkce,
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#433 04. 08. 2019 11:35 — Editoval vanok (04. 08. 2019 23:56)
Re: Limitny maraton
Pozdravy ↑ krakonoš:↑ check_drummer:,
Toto cvicenie sa da pochopitelne riesit viacerymi sposobmi.
Napr.
A) vyuzit a vysetrit differencialnu rovnicu 2y’+y=g(x)
B) pouzit funkciu h definovanu na  taku, ze h(x)=f(x). exp(x/2).
taku, ze h(x)=f(x). exp(x/2).
Pozrite na riesenie B) nasledujuce okienko.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#434 04. 08. 2019 23:54 — Editoval vanok (06. 08. 2019 20:37)
Re: Limitny maraton
Tak to riesenie B) ↑ vanok:.
Mame 2h’(x)/(2f’(x)+f(x))exp(x/2)
Predpoklad z textu cvicenia da ↑ vanok::  take, ze
take, ze 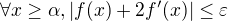
a tak 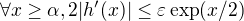
Na dokoncenie... ( urobim to cim skor)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#435 05. 08. 2019 11:50
#436 05. 08. 2019 12:22
Re: Limitny maraton
Ahoj ↑ krakonoš:,
No skor dokazes, ze je kladny nasobok exp(-x/2) je vädci ako f (x) ( pre  ako aj dokaze co som zacal v #434). A tiez aj keby si vyriesila cvicenie metodou A) pouzijes tu istu myslienku.
ako aj dokaze co som zacal v #434). A tiez aj keby si vyriesila cvicenie metodou A) pouzijes tu istu myslienku.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#437 05. 08. 2019 13:24
Re: Limitny maraton
↑ vanok:
I já původně viděla , že budou vyhovovat vztahu funkce y=0 a exponenciela exp(-x/2).
Tam je ale limita.Jsou ale i jiné funkce,které vztah splní např 1/x.Proto jsem na to šla nakonec obecně.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#438 06. 08. 2019 21:31 — Editoval vanok (07. 08. 2019 01:13)
Re: Limitny maraton
Pokracovanie #434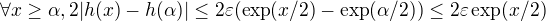
( vdaka skrytej poznamke v #434).
cize 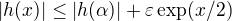 ,
,
co da 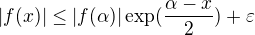 .
.
No vsak 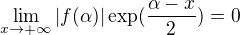 a tak existuje
a tak existuje  take, ze
take, ze 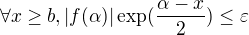 .
.
Cize  a konecne
a konecne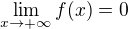
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#439 09. 08. 2019 14:17
Re: Limitny maraton
↑ vanok:
Ahoj
Připadá mi, že první řádek v #438 už vyplývá ze samotné definice derivace a vztahu .
.
Pokud je h rostoucí, pak funkce 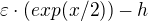 je neklesající.
je neklesající.
Pokud je h klesající, pak funkce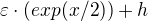 je neklesající.
je neklesající.
V případě h konstantní je to zřejmé.Všechny tyto případy vedou k platnosti vztahu
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#440 09. 08. 2019 14:36
Re: Limitny maraton
Ahoj ↑ krakonoš:,
V dokaze som pouzil “ théorème des accroissements finis”, pozri si ju napr. tu https://fr.m.wikipedia.org/wiki/Théor&# … ts_finis_2
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#441 09. 08. 2019 16:23
Re: Limitny maraton
↑ vanok:
Ahoj
Na to jsem se dívala včera, jde vpodstatě o aplikaci Cauchyho věty, která je důsledkem Rollovy věty.Jen mi připadalo , že tady nepotřebujeme použít,kolikrát větší derivace, tolikrát větší tangens na uzavřeném intervalu -že ta věta je možná zbytečně silná, a tedy by existoval jednodušší postup.Tady stačí, že když funkce má od .určitého okamžiku stále větší derivaci než ta druhá, pak i rozdíl hodnot má vždy větší
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#442 10. 08. 2019 09:12
Re: Limitny maraton
Cau ↑ krakonoš:,
Riesenie, ktore som oznacil B) ma vyhodu, ze je rychle.
No ked, chces mozes kludne pouzit aj variantu A), ktora popisana v #433, pouziva riesenie linearnej diferancielnej rovnice prveho radu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#443 10. 08. 2019 09:43 — Editoval krakonoš (10. 08. 2019 10:11)
Re: Limitny maraton
↑ vanok:
Ahoj
Já nemám zásadní výhrady k té metodě,ani k metodě přes separované proměnné,jen jsem chtěla poukázat,že je to vlastně pouhý důsledek definice derivace a monotonie, která z definice přímo vyplývá.Proč vlastně vidět za jednoduchými věcmi složitou teorii.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#444 10. 08. 2019 16:04
Re: Limitny maraton
Pozdravujem,
Problem (89).
Nech ![kopírovat do textarea $u_n= \frac 1n \sum_{k=1}^{n} \( [\frac {2n}k]-2[\frac nk] \)$](/mathtex/19/19728f7c3df0f5bf67aab989d970c44e.gif) , kde
, kde 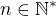
( [ ] ...oznacuje celu cast )
Urcite 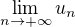 ( ak existuje).
( ak existuje).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#445 13. 08. 2019 09:28
Re: Limitny maraton
V ↑ vanok: mozte napriklad vyuzit, ze funkcia  definovana na
definovana na ![kopírovat do textarea $[0;1]$](/mathtex/43/43be75e2751ca361fc4f9d9353accecc.gif) definovana takto
definovana takto 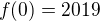 a pre
a pre ![kopírovat do textarea $x \in ]0;1],f(x)=[\frac 2x]-2[\frac 1x]$](/mathtex/e5/e5c1232c4bf30ac1eba171cacafdf3ba.gif) je Riemann-integrovatelna na intervale
je Riemann-integrovatelna na intervale ![kopírovat do textarea $[0;1]$](/mathtex/43/43be75e2751ca361fc4f9d9353accecc.gif) .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#446 13. 08. 2019 12:03 — Editoval krakonoš (13. 08. 2019 12:34) Příspěvek uživatele krakonoš byl skryt uživatelem krakonoš.
#447 13. 08. 2019 21:10 — Editoval krakonoš (13. 08. 2019 21:19) Příspěvek uživatele krakonoš byl skryt uživatelem krakonoš.
#448 14. 08. 2019 02:33 — Editoval vanok (14. 08. 2019 14:24)
Re: Limitny maraton
Pokracovanie ↑ vanok:,
Cize  je Riemann-ova suma a
je Riemann-ova suma a 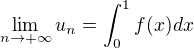
a mozme dokazat, ze sa rovna 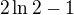
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#449 15. 08. 2019 16:21 — Editoval vanok (15. 08. 2019 16:36)
Re: Limitny maraton
Pokracovanie (89),
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#450 15. 08. 2019 16:40 — Editoval krakonoš (15. 08. 2019 18:16)
Re: Limitny maraton
↑ vanok:
Ale vždyť sám vidíš, že f(3/8)=1 podle výpočtu, ve skrytém textu #448 to však neodpovídá ani jednomu ze dvou případů.
Ten výpočet ve #449 je sice vpořádku, využíváš při výpočtu derivaci v kruhu konvergence, zpětné integrace a přejdeš na hranici konvergence, díky konvergence řady podle Abelova kriteria, tak jsem to aspoň pochopila,ale když nejsou správně předchozí kroky, k čemu je to dobré???
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
Stránky: 1 … 16 17 18 19 20 … 25
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Limitny maraton

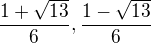 , korene charaktetistickej rovnice postupnosti su v interale
, korene charaktetistickej rovnice postupnosti su v interale ![kopírovat do textarea $]-1;1[$](/mathtex/47/47b4b74e3e5b4376c918e7140988d0d3.gif)
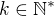 mame:
mame: tak
tak 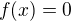
 tak
tak 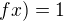 .
.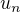 je Riemann-ova suma taka, ze
je Riemann-ova suma taka, ze 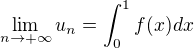 .
.
