Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#177 27. 11. 2018 13:59 — Editoval vanok (27. 11. 2018 13:59)
Re: Limitny maraton
Ahoj ↑ Marian:,
To je dobra cesta.
A konkretne je (napr.) zaujimave kuknut na 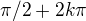 a tiez
a tiez 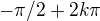 co da 2 vybrane postupnosti ....
co da 2 vybrane postupnosti ....
Necham citatelom to vyuzit.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#178 03. 12. 2018 15:06
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Limitny maraton
For a given sequence  If
If  Then
Then 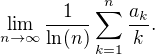 is
is
Offline
#179 03. 12. 2018 20:04 — Editoval vanok (03. 12. 2018 23:12)
Re: Limitny maraton
Hi ↑ stuart clark:,
Problem (46)
Look here
https://math.stackexchange.com/question … ca/3018729
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#180 04. 12. 2018 10:09
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Limitny maraton
Thanks ↑ vanok:. can you please explain me how i solve with stolz Theorem.
Offline
#181 04. 12. 2018 22:42
Re: Limitny maraton
Hi ↑ stuart clark:,
Here you will find theorem of Stolz Cesàro https://en.wikipedia.org/wiki/Stolz%E2% … ro_theorem .
The fixture taking as ------->
-------> 
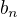 ------->
-------> 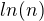
and 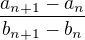 corresponding to
corresponding to 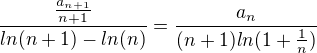
The rest is simple .
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#182 04. 12. 2018 23:22
#183 05. 12. 2018 04:38
#184 06. 12. 2018 06:03 — Editoval vanok (06. 12. 2018 22:41)
Re: Limitny maraton
HHi ↑ laszky:
You will find here http://forum.matweb.cz/viewtopic.ph … 90#p564890 in #4 a very instructive reading.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#185 08. 12. 2018 15:30
#186 09. 12. 2018 13:22
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Limitny maraton
@vanok can you please explain me how can i go further, Thanks
Offline
#187 10. 12. 2018 11:25 — Editoval vanok (13. 12. 2018 08:25)
Re: Limitny maraton
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#188 14. 12. 2018 07:03 — Editoval vanok (14. 12. 2018 07:04)
Re: Limitny maraton
Pozdravujem,
Tu najdete problem(47)
Urcite 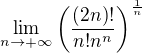 .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#189 14. 12. 2018 08:37
#190 14. 12. 2018 12:48
Re: Limitny maraton
Ahoj ↑ krakonoš:,
Odpoved je dobra.
No pacilo by sa mi vidiet riesenie, co pouzije Riemannove sumy.
Vies ako na to?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#191 14. 12. 2018 13:04 — Editoval krakonoš (14. 12. 2018 13:42)
Re: Limitny maraton
↑ vanok:
Asi to zlogaritmovat,castecne pokratit faktorialy a pak tam vzniknou souciny se n cleny,vyuzit ze logaritmus soucinu je soucet logaritmu,.....A integral z logaritmu od 1 do 2 spocist pres per partes,nakonec bude tam vznikne exp(vysledek integralu) t.j. vlastne odlogaritmovani.Zkousela jsem to a vyslo to stejne.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#192 14. 12. 2018 13:41
Re: Limitny maraton
↑ krakonoš:,
No myslienka je dobra, po ln dojdi k Riemannovej sume, ak ta to bavi skus to podrobne napisat ( to vies, ze ja nenechavam nikdy problemy bez riesenia, len aby som pomohol foristom).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#193 14. 12. 2018 13:45
#194 15. 12. 2018 12:17 — Editoval vanok (15. 12. 2018 17:08)
Re: Limitny maraton
Cau ↑ krakonoš:,
Tak pre kontrolu, tu dam to jednoduche riesenie, o ktorom som vyssie pisal. (↑ krakonoš: aby sa to lepsie citalo.)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#195 15. 12. 2018 14:57 — Editoval krakonoš (15. 12. 2018 15:06)
Re: Limitny maraton
↑ vanok:
Ahoj,
dívala jsem se na tvuj postup,ktery se sice trochu lisi od meho popsaneho,v zasade vsak vede ke stejnemu vysledku.Nejak se mi vsak nezdaji upravove kroky v celem druhem dlouhem radku.Aby platil posledni upravovy krok pred integraci ,
,
musela by predposledni suma bezet od n+1 nikoli od 1.Aspon si to myslim.
To byl i duvod,proc jsem ja radeji presla k upravam vyrazu jeste pred logaritmovanim,zdaly se mi pak jednodussi upravove kroky.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#196 15. 12. 2018 16:07 — Editoval vanok (15. 12. 2018 17:13)
Re: Limitny maraton
↑ krakonoš:,
Nejde o nic ine ako o substituciu i=k-n.
( Ak pochybujes, rozpis su vsetki cleny v kazdej  )
)
Inac opravil som maly preklep kde ma byt i =1, a nie I=1 a tiez som pridal jedno n, ako si to poznamenala ( no moj opravovac pravopisu automaticky robi opravy a niekedy to prehliadnem)
Poznamka: tu som pouzil Riemannove sumy ( normalne sa to vzdy ucilo v prvom rocniku VS, no mozno teraz na Sk, ci v Cz sa o tom uz vela nehovori .... ale podla mna ide o uzitocnu vec a tak ci tak to treba vediet .... a aj pouzit).
Skus pisat v LaTexe ja to robim aj na telefone bez velkych problemov.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#197 15. 12. 2018 19:11
Re: Limitny maraton
↑ vanok:
Já spíš vidím řešení odečíst ty dvě sumy, budu mít jen n členů a pak vzít n.log(n) a těchto n logaritmů přiřadit postupně do jmenovatelů členům.A dostanu rovnou předposlední úpravový krok.A tak dostanuposledni úpravový krok.
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
#198 15. 12. 2018 19:27 — Editoval vanok (15. 12. 2018 19:47)
Re: Limitny maraton
↑ krakonoš:, no akoze tam je n krat ln n, tak som od kazdeho od n clenov odpocital ln n.
Ale to je otazka organizacie vypoctov a tak je viacej ciest k rieeseniu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#199 16. 12. 2018 09:59 — Editoval vanok (16. 12. 2018 10:04)
Re: Limitny maraton
Pozdravujem,
Tu najdete problem (48)
Bez pouzitia Strirlingoveho vzorca vyrieste:
Polozme 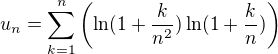 , kde n je prirodzene cislo
, kde n je prirodzene cislo  .
.
Najdite  ( ak existuje).
( ak existuje).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

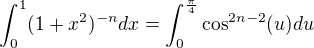 with substitution
with substitution 
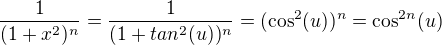
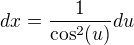
 ,then
,then 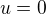
 , then
, then 
![kopírovat do textarea $ \int^{1}_{0}(1+x^2)^{-2}dx= \int_{0}^{\frac {\pi }4}\cos^2(u)du= \int_{0}^{\frac {\pi }4}\frac{1+cos(2u)}2du= \frac 12[u+\frac 12 \sin (2u)]_0^{\frac{\pi}2}=\frac 12(\frac{\pi}4+\frac 12)=$](/mathtex/1d/1d8f7b768488644a7cbd3690e2846ab5.gif)
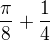
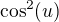
 , pre kazde nenulove prirodzene cislo.
, pre kazde nenulove prirodzene cislo.