Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Diferenciál u neurčitého integrálu (TOTO TÉMA JE VYŘEŠENÉ)
#1 17. 02. 2016 15:35
Diferenciál u neurčitého integrálu
Zdravím,
jaký význam má to "dx" u neurčitého integrálu?
U určitého mi to smysl dává, ale u neurčitého jsem to vždy vnímal pouze jako jakousi zarážku, že tady končí integrand. To ale asi není správné (např. když se musí přepočítat u substituční metody).
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
- (téma jako vyřešené označil(a) byk7)
#2 17. 02. 2016 17:19
Re: Diferenciál u neurčitého integrálu
Ahoj ↑ byk7:,
význam samo o sobě to nemá žádný, je to jen způsob, jak napsat primitivní funkci k f. Výhodu to má v tom, že můžeš vyznačit integrační proměnnou a taky to připomíná, že se s tím dá pracovat podobně jako s určitým integrálem (linearita).
Offline
#3 17. 02. 2016 21:12 — Editoval vanok (18. 02. 2016 02:16)
Re: Diferenciál u neurčitého integrálu
Ahoj ↑ byk7:,
Tu http://www.felderbooks.com/papers/dx.html
mas je den pohlad na tu otazku. Je to blizsie k fyzikom.
Inac pozri aj na historiu matematiky a na Leibniz-ove prace.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 17. 02. 2016 23:46
- check_drummer

- Příspěvky: 5167
- Reputace: 106
Re: Diferenciál u neurčitého integrálu
↑ byk7:
Ahoj, u intuitivních úvah to pomáhá, u formálních to mate. :-)
"Máte úhel beta." "No to nemám."
Offline
#5 18. 02. 2016 00:15 — Editoval Pavel (18. 02. 2016 00:15)
Re: Diferenciál u neurčitého integrálu
↑ Bati:
Pokud by "dx" nemělo žádný význam, pak by substituce v integrálech byla triviální záležitost. "dx" má historický význam, když se pan Leibniz zabýval nekonečně malými veličinami a ty označoval "dx", "dy" apod.
Nabízím dva své náhledy na význam objektu "dx" za integrálním znakem.
I. Definujme operátor diferenciálu funkce f jako
Definujme operátor 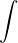 jako inverzní operátor k diferenciálu. Jsou-li
jako inverzní operátor k diferenciálu. Jsou-li  a
a  dvě funkce takové, že
dvě funkce takové, že 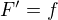 , pak
, pak  je primitivní k
je primitivní k  a platí
a platí
Tj. primitivní funkce  může být vyjádřena zápisem vpravo. Z toho by tedy vyplývalo, pokud jsou mé úvahy správné, že označení pro neurčitý integrál není jen
může být vyjádřena zápisem vpravo. Z toho by tedy vyplývalo, pokud jsou mé úvahy správné, že označení pro neurčitý integrál není jen 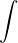 , ale
, ale 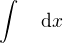 .
.
II. Vojtěch Jarník ve svém Integrálním počtu I definuje nejdříve Riemannův určitý integrál  . Dále zavádí pojem primitivní funkce pomocí vztahu
. Dále zavádí pojem primitivní funkce pomocí vztahu 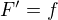 . Ukazuje, že funkce
. Ukazuje, že funkce 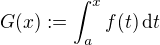 je jednou z primitivních funkcí k
je jednou z primitivních funkcí k  . A až následně definuje neurčitý integrál jako tuto primitivní funkci a zjednodušeně pro něj zavádí zápis
. A až následně definuje neurčitý integrál jako tuto primitivní funkci a zjednodušeně pro něj zavádí zápis 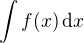 . Takže význam "dx" je převzat z teorie určitého integrálu.
. Takže význam "dx" je převzat z teorie určitého integrálu.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#6 18. 02. 2016 18:22
- check_drummer

- Příspěvky: 5167
- Reputace: 106
Re: Diferenciál u neurčitého integrálu
↑ Pavel:
Ahoj, dx má "fromálně" význam jen ten, že označuje jméno proměnné (x). Jinak bychom stejnš tak mohli zavést např. značení F(.,x), apod.
Používané značení má však historické jádro, jak píšeš.
"Máte úhel beta." "No to nemám."
Offline
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Diferenciál u neurčitého integrálu (TOTO TÉMA JE VYŘEŠENÉ)
