Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » taylorův rozvoj fce (TOTO TÉMA JE VYŘEŠENÉ)
#2 26. 05. 2009 22:57
Re: taylorův rozvoj fce
↑ Ginco:
Najprv zvolím substitúciu  . Potom počítam Maclaurinov rad funkcie
. Potom počítam Maclaurinov rad funkcie
To nebude ťažké, keďže  . Potom Maclaurinov rad je
. Potom Maclaurinov rad je
A teraz späť k subsitúcii
Chápeš?
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#3 26. 05. 2009 23:04
#5 26. 05. 2009 23:11
#8 06. 07. 2009 01:21
#10 07. 07. 2009 15:09
Re: taylorův rozvoj fce
↑ Rumburak:
díky moc, pěkně jsi to udělal a dobře mi to vysvětlil!
jen dopíši ten konec...
Offline
#11 07. 07. 2009 16:55
Re: taylorův rozvoj fce
↑ Ginco:
Výsledek mi vyšel stejně, ale mám dojem, že úprava (při převodu na spol. jmenovatele ve velké závorce) by správně měla být (podtrženo) .
.
Že se první chyba opravila další chybou v následujícím kroku, toť vzácný případ zázraku a chvíli jsem na to jen tupě zíral, nevěda, zda mi nehráblo ... :-)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » taylorův rozvoj fce (TOTO TÉMA JE VYŘEŠENÉ)
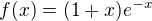 x_0 = -1
x_0 = -1

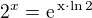
 :
: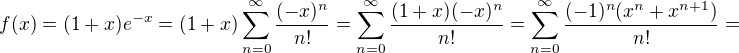
 .
.