Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 04. 2016 16:21
0.9 s periodou rovno 1
Napadlo mě, že by mezi 0.9 s periodou a 1 mohl být rozdíl 0.0...1 tj. 1 nekonečnina nebo něco takového. V tom případě by nemohlo platit 1/3 = 0.3...3, ale 0.3+1/30 nebo 0.33333+1/300000. 0.99...99 × 10 by bylo rovno 9.9...90. Potom 9.9...90 - 0.99...99 = 8.9...91 (jsem již poučen, že nekonečno - 1 = nekonečno, což respektuji, ale myslím, že to 2. nekonečno je o trochu menší). Pokud vynásobíme 0.99 × 10, tak za nekonečnem devítek bude prostě 0 (jako 11 × 10 = 110 a ne 111) , i když pokud je ta nula za desetinnou čárkou, tak se na ní snadno zapomene, zvláště pokud je na konci nekonečného desetinného rozvoje.
Moc toho zatím nevím, a předpokládám, že to moc velký smysl nedává. Prosím, aby mi někdo vysvětlil co a proč není tak, jak si představuji. Děkuji
Offline
- (téma jako vyřešené označil(a) wq)
#2 15. 04. 2016 20:54
Re: 0.9 s periodou rovno 1
↑ wq:
Liší-li se číslo 0.9 s periodou a 1 o "jednu nekonečninu", jak se bude od 1 lišit aritmetický průměr těchto dvou čísel? O polovinu nekonečniny?
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#6 16. 04. 2016 09:50
Re: 0.9 s periodou rovno 1
↑ wq:
asi myslíš "99...95 / 10 "na (nekonečnou + 1)" Protože nekonečno + 1 je nekonečno, tak by to znamenalo, že aritmetický průměr čísel 0.9 periodických a 1 by byl menší než obě tato čísla. Ale aritmetický průměr leží mezi nimi přesně uprostřed.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#8 16. 04. 2016 11:40
Re: 0.9 s periodou rovno 1
↑ wq:
Problém však zůstává. Pokud spočítám dle Tvých úvah průměr, tak ten bude menší než 0.9 periodických a 1, což není dost dobře možné.
Ty s nekonečnem pracuješ jako s přirozeným číslem, ale nekonečno do množiny přirozených čísel nepatří. Proč si myslíš, že pro něj budou platit stejné zákonitosti jako pro počítání s přirozenými čísly? Z čeho plyne Tvoje úvaha, že nekonečno-1 je o trochu menší než nekonečno?
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#9 16. 04. 2016 12:55 — Editoval wq (16. 04. 2016 13:18)
Re: 0.9 s periodou rovno 1
Moje úvaha plyne právě z toho, že když odečtu 1, pak je rozdíl mezi menšencem a výsledkem právě 1.
Pokud a - 1 = b, přičemž a = nekonečno, tak b = nekonečno, jenže a - b = 1. V našem případě nesmíme chápat nekonečno jako přímku bez začátku i bez konce, ale ani jako polopřímku - zkus to třeba brát jako zázračnou lampu, která, aniž by jí praskla žárovka dokáže bliknout po 30s, pak po 15s, dál po 7,5s a vždy po polovině předchozího časového intervalu. Otázka zní: "Kolikrát lampa blikne za jednu minutu?". Myslíš, že se zastaví, resp. nekonečně zpomalí čas? Já myslím, že prostě blikne nekonečnokrát.
Podle mého, můžeme někdy nekonečno ohraničit dvěma nekonečně vzdálenými body.
A konečně k tomu problému - "..." označuje nekonečno devítek a každá další devítka představuje další desetinné místo,
tzn. 0.99...9 = 0.99...90 a 0.99...90 < 0.99...95.
Offline
#11 16. 04. 2016 18:09
Re: 0.9 s periodou rovno 1
Není nekonečno, jako nekonečno. Pokud a = nekonečno,
tak a - a = 0 a ne 1. Já jsem odčítal a - b, b = a - 1= nekonečno - 1 = nekonečno. a,b jsou nekonečna, ale a>b. Řekněme, že b není přímo "Nekonečno", ale jiná "nekonečná hodnota", konkrétně "Nekonečno mínus jedna".
Offline
#12 16. 04. 2016 21:13
Re: 0.9 s periodou rovno 1
↑ wq:
A číslo 0.9 periodických obsahuje "nekonečně mnoho" devítek nebo "nekonečně +1" mnoho devítek?
Problém je v tom, jak definuješ nekonečno. Buď jaksi intuitivně, pak si každý pod nekonečnem může představit cokoliv, nebo jako speciální matematický objekt, který je větší než jakékoliv reálné číslo. Pokud se neshodneme nad obsahem pojmu nekonečna a každý si pod ním bude představovat něco jiného, nemá smysl rozebírat věci s nekonečnem související.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#13 16. 04. 2016 22:04
Re: 0.9 s periodou rovno 1
↑ Pavel:
Jen "nekonečně mnoho" devítek. Vlastně jsem se dopustil nepřesnosti, když jsem prohlásil, že "..." je nekonečno devítek. Ono je to spíš nekonečno-3 devítek v případě, že napíšu 0,99...9.
Celou dobu jsem se snažil vám vysvětlit, jak já pojem nekonečno vnímám, ale jelikož navštěvují teprve 7. ročník ZŠ, tak nechtěj, abych vám tady vykládal něco o tom, jestli je nekonečno reálné číslo apod. .
Mě spíš zajímá, jestli je nějaký jiný důkaz o tom, že 0.9 s periodou = 1, který nemůžu podobným způsobem zpochybnit, a který bych i já pochopil.
Offline
#15 16. 04. 2016 23:23
Re: 0.9 s periodou rovno 1
↑ byk7:
No právě - jak už jsem napsal, 10.11=110 a ne 111 - nemůžeš tu jedničku vzít jentak z ničeho. a ne
a ne 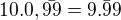

Důvod, proč píšu  místo
místo je to, aby jste lépe pochopili, že nejdřív je za des. č.
je to, aby jste lépe pochopili, že nejdřív je za des. č.  devítek, a když to vynásobíme .10 tak je to
devítek, a když to vynásobíme .10 tak je to  devítek (1 devítka je před des. č.).
devítek (1 devítka je před des. č.).
Offline
#16 16. 04. 2016 23:42
Re: 0.9 s periodou rovno 1
↑ wq: Nie, tu deviatku, respektive jednotku v tvojom pripade nevezmes z nicoho nic, ale vezmes ju z toho, ze ten desatinny rozvoj je nekonecny a vzdy tam bude dalsia deviatka. A presne preto pri nasobeni cislom 10 nevznikne nakonci 0, ale objavi sa tam dalsia 9 a posunie sa desatinna ciarka.
Podobny, ale trosku iny dokaz: 
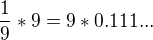

Offline
#17 16. 04. 2016 23:57 — Editoval misaH (17. 04. 2016 00:06)
- misaH
- Příspěvky: 13459
Re: 0.9 s periodou rovno 1
↑ Kenniicek:
Nemá význam, škoda času...
On to veľmi dobre vie, je to preňho ale o "inom nekonečne" ako ho vidíš ty.
Lebo podľa neho keď z nekonečná vezmeš 1, tak už je to iné nekonečno než predtým, menšie o tú 1 ...
Naozaj škoda času.
Nevie pochopiť, že rátať s nekonečnom ako s číslom sa nedá. Podľa mňa vôbec žiadnu teóriu o nekonečne nepozná a tipujem, že ho ani nezaujíma.
No ale možno máme pred sebou budúceho nositeľa Nobel ovej ceny, ktovie...
Offline
#18 17. 04. 2016 00:04 — Editoval Kenniicek (17. 04. 2016 00:09)
Re: 0.9 s periodou rovno 1
↑ misaH:
Nechcem aby to vyznelo zle, ale ja sa mu nedivim, ze to nechape a nevidi ako my. Nie je vela ludi, ktori by to pochopili v 7. rocniku zakladnej skoly. Ale na druhu stranu, mohol by nam trosku verit :)
↑ wq:
Mozno toto ti trosku pomoze: https://cs.wikipedia.org/wiki/Roz%C5%A1 … D%C3%ADsla
Offline
#19 17. 04. 2016 00:06 — Editoval misaH (17. 04. 2016 00:14)
- misaH
- Příspěvky: 13459
Re: 0.9 s periodou rovno 1
↑ Kenniicek:
:-)
Mohol a nemohol ... nech si robí čo chce a teší sa zo života.
https://cs.m.wikipedia.org/wiki/Nekonečno
Slovenská wiki je stručnejšia a myslím že zrozumiteľnejšia.
Z nekonečna sa vraj niekoľko matematikov zbláznilo, ale neviem, či to je pravda...
Offline
#20 17. 04. 2016 00:56 — Editoval Eratosthenes (17. 04. 2016 00:58)
- Eratosthenes
- Příspěvky: 2784
- Reputace: 137
Re: 0.9 s periodou rovno 1
ahoj ↑ wq:,
je od Tebe sice hezké, že si už v tomto věku kladeš takové otázky, na druhé straně pochop, že v 7. třídě ZŠ některým věcem z matematiky ještě rozumět nemůžeš. A prozatím se smiř s tím, že 0.9 periodických a jednička je jedno a totéž.
Budoucnost patří aluminiu.
Offline
#24 17. 04. 2016 19:30
- Eratosthenes
- Příspěvky: 2784
- Reputace: 137
Re: 0.9 s periodou rovno 1
↑ Kenniicek:
>> taktiez v praxi nefunguje matematicke nekonecno.
Ale právě paradox Achila a želvy dokazuje, že nekonečno v praxi funguje. Zrovna tento "paradox" je totiž paradoxem jen pro toho, kdo pojem nekonečna nechápe...
Budoucnost patří aluminiu.
Offline

 , tj.
, tj.  , což v kombinaci s tvým výsledkem dá
, což v kombinaci s tvým výsledkem dá  . To už je objektivně špatně, ne?
. To už je objektivně špatně, ne? , pak
, pak  , tj.
, tj.  a odtud
a odtud  .
.