Matematické Fórum

hanos · 30. 05. 2009 14:30

zadání příkladu je - Vypočtěte všechny 1. a 2. derivace funkce $f(x,y)=(x+2y)\sqrt y$
Prosím kdyby mi mohl někdo poradit. A jestli někdo neví o nějakém odkazu na webové stránky, kde bych to mohl nastudovat. Parciálni derivace mi dělají problémy. Děkuji

Marian · 30. 05. 2009 14:34 — Editoval Marian (30. 05. 2009 14:34)

↑ hanos:
A umíš zderivovat funkci jediné proměnné, třeba
$g(x)=(x+2\pi)\cdot\sqrt{\pi},$
nebo obecněji
$g(x)=(x+2c)\cdot\sqrt{c},$
kde "c" je nějaká (kladná) konstanta? Pokud nikoliv, musíš hledat příčinu nezvládnutí parciálního derivování v nezvládnutí klasického derivování, protože - de facto - nic nového to není.

hanos · 30. 05. 2009 15:00

↑ Marian:
takže $f(x)=0$
??????

lukaszh · 30. 05. 2009 15:10

↑ hanos:
Fakt tu budú problém nie len s parciálnym derivovaním, ale aj s derivovaním ako takým. Neviem, odkiaľ si vzal, že f(x)=0. Je tu funkcia dvoch premenných. Idem na to úplne primitívne a formálne nesprávne. Pod y chápem konštantu, napríklad tú Marianovu odmocninu $\sqrt{\pi}$ , čo je iba číslo. Nič iné. Je trochu špecifické, aby som ho potom spätne vedel rozoznať. Idem derivovať funkciu dvoch premenných podľa x:
$f(x,y)=x^2y+xy$
Keď ti to pomôže, i keď by ma za to vyhodili zo skúšky, tak:
$f(x,\sqrt{\pi})=x^2\sqrt{\pi}+x\sqrt{\pi}$
Toto derivované podľa x, je ako primitívna derivácia podľa x pre funkciu jednej premennej. Odporúčam "nabifliť sa" veeeľmi ťažký vzorec 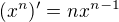$(x^n)'=nx^{n-1}$
$f'_x(x,\sqrt{\pi})=(x^2\sqrt{\pi})'+(x\sqrt{\pi})'=2x\sqrt{\pi}+1\cdot\sqrt{\pi}$
Teraz dosadím za to pi pôvodné y
$f'_x(x,y)=(x^2y)'+(xy)'=2xy+y$
To je až také ťažké?

hanos · 30. 05. 2009 15:31 — Editoval hanos (30. 05. 2009 16:09)

↑ lukaszh:
jsem myslel, že pokud se y uvažuje jako konstanta, tak že potom bude y po zderivování 0, ale jak sem si všimnul, tak konstantu jsi opisoval, takže podle toho jsem došel k výsledku

Je to správně????

Ivka987 · 30. 05. 2009 19:38

Prosím o pomoc s parciální derivací z´x u příkladu

x-y
arctg ---------
1 + xy

1 (1+xy) - (x-y)*(y)
Vím, že to je: ------------ * ------------------------
1 + (x-y)^ 2 (1 +xy) ^ 2
------
(1+xy)^ 2

ale dál nevím..Díky

made001 · 30. 05. 2009 19:46

Dál to stačí už jen algebraicky upravit. Převést na společného jmenovatele, vykrátit, co se dá atd.

lukaszh · 30. 05. 2009 19:57

↑ hanos:
Áno, problém je skutočne v derivovaní funkcie jednej premennej. Zopakuj si základy, potom sa pusti do parciálneho derivovania. Je potrebné pochopiť, ako to funguje. Určite neplatí, že $(3x)'=0$ , pretože 3 je konštanta. Platí jedine $(3)'=0$ , pretože je to konštanta sama o sebe. Okrem toho, ak to nechápeš tak
$(3x)'=(x+x+x)'=(x)'+(x)'+(x)'=1+1+1=3$
Takže konštanta nekonštanta, nula to nie je.

Ivka987 · 30. 05. 2009 20:05

↑ made001:

To vím..ale nejde mi to..nemůžu se dostat k výsledku.. Napsal bys mi prosím postup?

xificurC · 30. 05. 2009 20:26

↑ hanos:
Tvoj vysledok vyzera asi tak, ako keby si najprv za x dosadil jednotku a potom opisal celu funkciu este raz. Preto skusim vysvetlit zaklady aj ja. Mas funkciu $f(x,y)=x\sqrt{y}+2y^{\tiny \frac{3}{2}}$ , ktorej chces vsetky prve a druhe derivacie. Takze skusme najprv prvu podla x: spravne znacenie je nasledovne: $f_x'(x,y)$ a parcialna derivacia sa vyrata tak, ze celu funkciu zderivujes podla premennej x. Teda prvy clen je x odmocnina z y, pricom teraz ako premennu beries len x, co pre Teba znamena tolko, ze y je len cislo, resp. je zafixovane. Derivaciu x vypocitas podla vzorcov, ktore ste sa urcite ucili a ten potrebny uz Lukaszh aj napisal, $(x^n)'=nx^{n-1}$ . 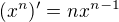n je v tomto pripade 1 takze Tvoj vysledok je $\sqrt y\cdot 1\cdot x^{1-1}=\sqrt y$ , teda prvy clen sa zderivoval na odmocninu z y. Druhy clen je bez premennej x, teda z pohladu x-ov je to konstanta, ktora sa zderivuje na nulu. Teda $f_x'(x,y)=\sqrt{y}$ . Ak si pochopil vykladu, parcialnu derivaciu podla y budes vediet napisat, takze schvalne skus :) Kedze od Teba pytaju aj druhe derivacie, po vypocte prvych parcialnych obe vysledky znovu zderivujes aj podla x aj podla y. Teda parcialnu podla x tu uz mas vyratanu ako odmocninu z y, tento vysledok zderivujes podla x (kde Ti vyjde 0) aj podla y (pouzijes vyssie spomenuty vzorec). Pre mensiu kontrolu posluzi aj to, ze plati rovnost $f_{xy}''(x,y)=f_{yx}''(x,y)$ . Vela stastia :)

jelena · 31. 05. 2009 01:23

↑ Ivka987:

$\mathrm{arctg {\frac{x-y}{1 + xy}}}$

úprava parciální derivace po x (:

$\frac{1}{1+\left(\frac{x-y}{1 + xy}\right)^2} \cdot {\frac{1 + xy-y(x-y)}{ (1 + xy)^2}}=\frac{(1 + xy)^2}{(1 + xy)^2+(x-y)^2} \cdot {\frac{1 + xy-xy+y^2}{ (1 + xy)^2}}=\nl \nl=\frac{1}{1 + 2xy+(xy)^2+x^2-2xy+y^2} \cdot {\frac{1 + y^2}{1}}=\nl \nl=\frac{1}{1 + (xy)^2+x^2+y^2} \cdot {\frac{1 + y^2}{1}}=\frac{1}{1+y^2+x^2(1+y^2)} \cdot {\frac{1 + y^2}{1}}=\nl \nl=\frac{1}{(1+y^2)(x^2+1)} \cdot {\frac{1 + y^2}{1}=\frac{1}{x^2+1$

-----------

čim se dá bavit, однако

hanos · 31. 05. 2009 12:19

↑ xificurC:
ok, takže $f(x,y)=(x+2y)\sqrt y$ po zderivování podle x se bude rovnat $f_x(x,y)=sqrt y$ teda pokud se nepletu?

Johny · 31. 05. 2009 13:03 — Editoval Johny (31. 05. 2009 13:03)

↑ hanos:

Přesně tak . Jo a kdyby ses koukl do prvního tématu, tak by si todle nemuisel zakládat.

Majkky · 31. 05. 2009 21:07

Potrebujem pomoc pri výpočte tejto parciálnej derivácie

4x-2
z₌(5y+3)

Diki pekne

Johny · 31. 05. 2009 21:17

↑ Majkky:

Koukni zde : http://user.mendelu.cz/marik/maw/index. … m=derivace

Majkky · 31. 05. 2009 21:20

↑ Johny:

Diki kamo :)

Marian · 31. 05. 2009 21:26

↑ hanos:↑ lukaszh:

Doporučuji rozlišovat dva druhy konstant
(a) aditivní,
(b) multiplikativní.

Příklad k (a):
$f(x)=\boxed{301+}x,\qquad g(x)=\boxed{401-}x$
příklad k (b):
$g(x)=\boxed{301\cdot }x,\qquad g(x)=\frac{x}{401}=\boxed{\frac{1}{401}\cdot }x.$

Jednou se u derivování konstanta opisuje (multiplikativní konstanta), jednou se neuvažuje (po derivaci je nula - aditivní případ).

Matematické Fórum

#1 30. 05. 2009 14:30

Parciální derivace

#2 30. 05. 2009 14:34 — Editoval Marian (30. 05. 2009 14:34)

Re: Parciální derivace

#3 30. 05. 2009 15:00

Re: Parciální derivace

#4 30. 05. 2009 15:10

Re: Parciální derivace

#5 30. 05. 2009 15:31 — Editoval hanos (30. 05. 2009 16:09)

Re: Parciální derivace

#6 30. 05. 2009 19:38

Re: Parciální derivace

#7 30. 05. 2009 19:46

Re: Parciální derivace

#8 30. 05. 2009 19:57

Re: Parciální derivace

#9 30. 05. 2009 20:05

Re: Parciální derivace

#10 30. 05. 2009 20:26

Re: Parciální derivace

#11 31. 05. 2009 01:23

Re: Parciální derivace

#12 31. 05. 2009 12:19

Re: Parciální derivace

#13 31. 05. 2009 13:03 — Editoval Johny (31. 05. 2009 13:03)

Re: Parciální derivace

#14 31. 05. 2009 21:07

Re: Parciální derivace

#15 31. 05. 2009 21:17

Re: Parciální derivace

#16 31. 05. 2009 21:20

Re: Parciální derivace

#17 31. 05. 2009 21:26

Re: Parciální derivace

Zápatí