Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 05. 2016 21:02
- Crashatorr
- Příspěvky: 360
- Reputace: 7
Důkaz u funkcionálů
Zdravím, byl by ochotný mi někdo pomoci prosím ?
Snažím pochopit důkaz u Hahn-Banach věty a nemohu dokázat jednu věc je reálný lineární prostor,
je reálný lineární prostor,  je jeho podprostor,
je jeho podprostor, 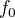 je lineární funkcionál v
je lineární funkcionál v  ,
,  je konečný konvexní funkcionál v
je konečný konvexní funkcionál v  , přičemž
, přičemž kde
kde 
Nechť , pak vzhledem k
, pak vzhledem k  a konvexnosti p pro
a konvexnosti p pro
 , kde
, kde 
Nechť 

A nevím jak dokázat 
Offline
#2 21. 05. 2016 00:05
Re: Důkaz u funkcionálů
Ahoj ↑ Crashatorr:,
pokud  pro všechny
pro všechny 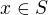 , pak
, pak  . To plyne z definice suprema. Podobně pro infimum.
. To plyne z definice suprema. Podobně pro infimum.
Offline
#3 21. 05. 2016 20:46
- Crashatorr
- Příspěvky: 360
- Reputace: 7
Re: Důkaz u funkcionálů
Šlo by to i tak?
Stačí ukázat že  platí
platí
Ale vidím, že 
Offline
