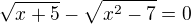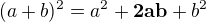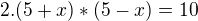Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 24. 05. 2016 14:52 — Editoval Blackflower (24. 05. 2016 14:55)
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Iracionání rovnice
↑ steve95: Ahoj,
prehoď jednu z odmocnín na ľavú stranu, umocni celú rovnicu na druhú, prehoď všetko na jednu stranu a dostaneš polynóm druhého stupňa. Bude mať dva korene a treba overiť, či po dosadení do rovnice nevznikne záporné číslo pod odmocninou.
EDIT: oprava+doplnenie
Offline
#3 24. 05. 2016 14:56
Re: Iracionání rovnice
↑ Blackflower:
Měla to být jiná rovnice, omlouvám se :
Tamta mi vyšla,jen jsem spletl za tuto
Offline
#4 24. 05. 2016 15:01
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Iracionání rovnice
↑ steve95: Umocni celú rovnicu na druhú. Dosť vecí ti tam povypadáva a rovnica sa dosť zjednoduší.
Offline
#6 24. 05. 2016 15:05
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Iracionání rovnice
↑ steve95: Po umocnení tam ostane aj x. Ak chceš, napíš sem svoj postup a nájdeme chybu.
Offline
#8 24. 05. 2016 15:09 — Editoval Blackflower (24. 05. 2016 15:10)
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Iracionání rovnice
↑ steve95: Ešte ti tam chýba člen  .
.
Offline
#10 24. 05. 2016 15:13
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Offline
#11 24. 05. 2016 15:13 — Editoval Al1 (24. 05. 2016 15:15)
Re: Iracionání rovnice
↑ steve95:
Zdravím,
a nezapomeň na zkoušku, umocnění není ekvivalentní úprava.
U této rovnice lze řešení ihned vidět.
Offline
#13 24. 05. 2016 15:22
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Iracionání rovnice
↑ steve95: Kde konkrétne je problém?
Offline
#15 24. 05. 2016 15:30
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Iracionání rovnice
↑ steve95: Nie, asi sme sa nepochopili.
Podľa vzorca 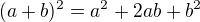 umocníme celú rovnicu a dostaneme:
umocníme celú rovnicu a dostaneme: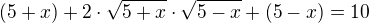
Päťky naľavo sa vynulujú s desiatkou napravo, takisto sa vynuluje  a
a  naľavo. Teda nám ostane toto:
naľavo. Teda nám ostane toto:
Vydelíme dvojkou: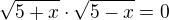
Offline
#17 24. 05. 2016 15:34
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Iracionání rovnice
↑ steve95: Áno, rovnica má tieto dve riešenia. Vo všeobecnosti ale treba overiť, či všetky nájdené riešenia môžeme spätne dosadiť do rovnice, aby sme sa vyhli zápornému číslu pod odmocninou - o tom píše aj ↑ Al1:.
Offline
#19 24. 05. 2016 15:37
- Blackflower


- Místo: Bratislava
- Příspěvky: 1303
- Škola: FMFI UK BA, EFM, absolvent 2016
- Pozice: aktuár
- Reputace: 71
Re: Iracionání rovnice
↑ steve95: Neboj, do toho sa dostaneš, chce to len tréning.
Offline