Matematické Fórum

Agil · 14. 08. 2016 13:24

Zdravím, absolutně netuším, jak postupovat. Zkoušel jsem to nějak rozložit pomocí vytíkání, ale nic.
Děkuji
//forum.matweb.cz/upload3/img/2016-08/73827_ko%25C5%2599eny.JPG

Blackflower · 14. 08. 2016 13:44

↑ Agil: Ahoj,
skús vyňať z prvých dvoch členov 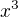$x^3$ a z druhých dvoch členov dvojku.

Agil · 14. 08. 2016 14:11 — Editoval Agil (14. 08. 2016 14:13)

↑ Blackflower:

$x^{3}\cdot (2x^{2}+1)-2\cdot (x^{2}-1)$

Takto? Bohužel, stále nevím, co s tím.
$x^{3}\cdot (2x^{2}+1)-2\cdot (x-1)\cdot (x+1)$

misaH · 14. 08. 2016 14:28 — Editoval misaH (14. 08. 2016 14:30)

$x^{3}\cdot (2x^{2}+1)-2\cdot (x^{2}-1)$

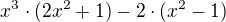
Takto nie. Veď si to roznásob nazad.

Neurobí sa ti 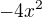$-4x^2$ ani $-2$ .

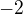Mínus krát mínus je plus.

Agil · 14. 08. 2016 14:36

↑ misaH:

Nojo, máš pravdu.

$x^{3}\cdot (2x^{2}+1)-2\cdot (2x^{2}+1)$

$(2x^{2}+1)\cdot (x^{3}-2)$

A teď tedy, první závorka se nikdy nemůže rovnat nule.
A druhá se rovna nule, pro $\sqrt[3]{2}$
Díky.

Matematické Fórum

#1 14. 08. 2016 13:24

Kořeny polynomu

#2 14. 08. 2016 13:44

Re: Kořeny polynomu

#3 14. 08. 2016 14:11 — Editoval Agil (14. 08. 2016 14:13)

Re: Kořeny polynomu

#4 14. 08. 2016 14:28 — Editoval misaH (14. 08. 2016 14:30)

Re: Kořeny polynomu

#5 14. 08. 2016 14:36

Re: Kořeny polynomu

Zápatí