Matematické Fórum

BakyX · 20. 08. 2016 19:57

Dobrý deň.

Ako exaktne dokázať, že ak máme spojitú prostú funkciu, tak jej inverzná funkcia je spojitá?

Ďakujem.

Bati · 21. 08. 2016 00:57

Ahoj ↑ BakyX:.
Jedna možnost:

Z věty o nabývání mezihodnot spojité funkce plyne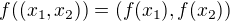
$f((x_1,x_2))=(f(x_1),f(x_2))$ (případně $=(f(x_2),f(x_1))$ ).
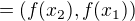Navíc, kvůli prostotě $f=(f^{-1})^{-1}$ .
Vidíme tedy, že vzory ot. intervalů při zobrazení $f^{-1}$ jsou ot. množiny (dokonce ot. intervaly). A to stačí, protože ot. intervaly tvoří bázi standardní topologie v $\mathbb{R}$ .

vanok · 22. 08. 2016 09:06 — Editoval vanok (22. 08. 2016 09:12)

Ahoj ↑ BakyX:,
Tu https://msuhonorsanalysis.wordpress.com … functions/
mas vysetrenu pytanu situaciu, a dokonca da odpoved aj co da tyka derivacie ( i ked nie v uplne vseobecnej konfiguraciu , ale ktora ti da klucove myslienky v najbeznejsich situaciach)
Pozor, ak pouzivas bezne konvencie tak $f^{-1}$ existuje len v pripade ked $f$ je bijektivna.

Rumburak

↑ BakyX:

Ahoj. (Zdravím i ostatní účastníky diskuse) .

Jiný (elementárnější) postup.

Doplnil bych větu o předopoklad , že definičním oborem oné prosté spojité funkce $f$ je interval - označme ho $I$ .
Odtud vyplyne, že $f$ je rostoucí nebo klesající a oborem jejích hodnot je rovněž interval - označme ho $J$ .
Funkce $f^{-1}$ tedy bude rostoucí resp. klesající funkcí zobrauijící interval $J$ na interval $I$ .

Když dokážeme, že pro libovolnou monotonní posloupnost $(y_n)$ bodů z $J$ mající limitu $y \in J$ platí

$\lim_{n \to \infty} f^{-1}(y_n) = f^{-1}(y)$ ,

budeme s důkazem spojitosti funkce $f^{-1}$ v bodě $y$ v podstatě (až na pár zbývajících maličkostí) hotovi .

Matematické Fórum

#1 20. 08. 2016 19:57

Spojitosť inverznej funkcie

#2 21. 08. 2016 00:57

Re: Spojitosť inverznej funkcie

#3 22. 08. 2016 09:06 — Editoval vanok (22. 08. 2016 09:12)

Re: Spojitosť inverznej funkcie

#4 22. 08. 2016 10:20 — Editoval Rumburak (22. 08. 2016 10:48)

Re: Spojitosť inverznej funkcie

Zápatí