Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 03. 06. 2009 13:14 — Editoval musixx (03. 06. 2009 13:15)
Re: Příjmačky na VŠE
Není zdaleka jediná cesta, jak tohle zdůvodnit. Například si na intervalu (0,pi) představíš (či načrtneš) graf funkce cosinus, vidíš, že je to tam spojitá klesající funkce nabývající všech hodnot mezi -1 a +1, a tedy právě jednou také nabude kýžené hodnoty 1/3. Proto je odpověď "jedna". Vyčíslit to x, to je už poněkud těžší, protože ta 1/3 není cosinus žádného "běžně známého úhlu"- ale to se po nás nechce, píšu to jen jako takovou poznámku.
Offline
#9 03. 06. 2009 13:58 — Editoval musixx (03. 06. 2009 13:59)
Re: Příjmačky na VŠE
↑ Pí: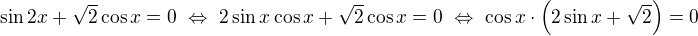 . Cinitel
. Cinitel 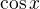 je na (0, pi) nulovy jen pro
je na (0, pi) nulovy jen pro  a cinitel
a cinitel  neni na zadanem intervalu nulovy nikdy, protoze rovnice
neni na zadanem intervalu nulovy nikdy, protoze rovnice 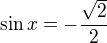 nema na
nema na  zadne reseni. Proto je jednine reseni, tedy vysledek 1.
zadne reseni. Proto je jednine reseni, tedy vysledek 1.
EDIT: Cheop byl o nejakou tu vterinku rychlejsi. :-)
Offline
#15 03. 06. 2009 14:49 — Editoval musixx (03. 06. 2009 14:51)
Re: Příjmačky na VŠE
↑ Pí: Nulové body jsou 1 a 3. Na intervalu  tedy jde o nerovnost
tedy jde o nerovnost  , tedy
, tedy  , tedy
, tedy  , tedy první částí definičního oboru je interval
, tedy první částí definičního oboru je interval  . Na intervalu
. Na intervalu  jde o nerovnost
jde o nerovnost  , tedy
, tedy  , tedy
, tedy  , tedy druhou částí definičního oboru je interval
, tedy druhou částí definičního oboru je interval 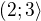 . Na posledním intervalu
. Na posledním intervalu 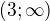 jde o nerovnost
jde o nerovnost  , tedy
, tedy  , tedy třetí částí definičního oboru je inteval
, tedy třetí částí definičního oboru je inteval 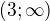 . Druhý a třetí interval definičního oboru jde zapsat společně, tedy definiční obor je
. Druhý a třetí interval definičního oboru jde zapsat společně, tedy definiční obor je  (pokud jsem se teda někde nespletl).
(pokud jsem se teda někde nespletl).
Offline
#17 03. 06. 2009 15:55
Re: Příjmačky na VŠE
Ahoj, taky dělám příjmačky na VŠE a narazil jsem na zápis, kterému moc nerozumím, jestli by mě mohl někdo říct o co se vlastně jedná. Maturoval jsem za 1, a na jiné fakutlě VŠ jsem udělal Matematiku za 2, ale tohle fakt vidim poprvé.
Prosím pomozte mi, děkuju moc!!!!!!!!!!!!! Fakt to nemužu nikde najít.
Offline
#18 03. 06. 2009 16:18 — Editoval jelena (03. 06. 2009 16:19)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Příjmačky na VŠE
↑ Kjuba:
http://forum.matweb.cz/viewtopic.php?id=7540&p=2 nebo 4. řádek ze základních vlastnosti- je potřeba přehodit na levou stranu.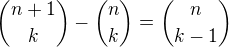
ale kdo si to ma pamatovat, že kolego halogane :-)
-------
Proč každý chce na VŠE?
Offline
#21 03. 06. 2009 16:32
Re: Příjmačky na VŠE
↑ Pí: Pokud je tohle jako vysledek, tak jsou dve moznosti: mas spatne zadani nebo je vzorovy vysledek spatne. Dosad si treba -2.5 a uvidis, ze spada do definicniho oboru, a dosad si treba 2.1 a uvidis, ze take spada do definicniho oboru.
Offline

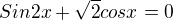




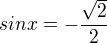


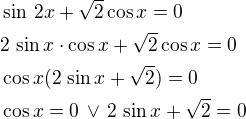



 - 1 řešení
- 1 řešení . Umíš tohle řešit třeba přes tzv. nulové body?
. Umíš tohle řešit třeba přes tzv. nulové body? , po úpravě tedy
, po úpravě tedy  .
.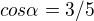

 ?? pač v příjmačkách to po mě chtějí :(
?? pač v příjmačkách to po mě chtějí :( ?
?