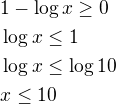Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#34 03. 06. 2009 22:46 — Editoval Kjuba (03. 06. 2009 22:48)
Re: Příjmačky na VŠE
Dělal jsem si test nanečisto a tomuhle FAKT nerozumim, vždyť reálná čísla mohou být záporná ne?
Za předpokladu např 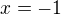
potom
3^(-1)<1 sorry tenhle výraz mi Tex nechtěl vzít...
Ale ve výsledku má vyjít prázná množina, jsem z toho jelen.
Btw: jak udělám další řádek v Texu?
Offline
#35 03. 06. 2009 23:02 — Editoval Marian (03. 06. 2009 23:02)
Re: Příjmačky na VŠE
↑ Kjuba:
Žádná z předchozích možností - to je správná odpověď. Pokud správně vidím, tak u první možnosti překáží pravý hraniční bod intervalu. Pro nulu už tvrzení neplatí. Čtvrtá možnost má správnému výsledku celkem blízko, ale nejsou ta všechna čísla, chybí interval [-1,0).
V TeXu musíš napsat toto (není to možná dobře čitelné, ale jsou tam složené závorky {...})
Code:
[tex]
3^{-1}<1
[/tex]Další řádek uděláš tak, že použiješ příkaz \\, tedy dvě obrácená lomítka (+ eventuálně Enter nebo mezera).
Offline
#37 03. 06. 2009 23:17
Re: Příjmačky na VŠE
Pak je tedy správná první možnost. Že bych ale neviděl správně si nemohu vyčítat - ono je to nečitelné. Je velká škoda, že mnoho lidí, kteří vyučují matematice, neumí použít adekvátní prostředek k jejímu zápisu - lze akceptovat pouze (La)TeX jakožto synonymum nejvyšší kvality (pozn. pro méně zkušené - tady na fóru formulky v TeXu nevypadají tak hezky, jak je tomu ve vygenerovaném PDF).
Offline
#43 04. 06. 2009 14:54
- kubistation
- Zelenáč
- Příspěvky: 21
- Reputace: 0
Re: Příjmačky na VŠE
ahoj nevím si rady s tímto příkladem:-( imaginární část koplexního čísla z: 1 - i + i^2 - i^3 -i ^4 - i^5 je rovna tomuto číslu Jako imaginární část jsem vzala všechny ička a nemůžu se jich zbavit,jedno mi zbývá. výsledek má být -1
A potom ještě z jiného soudku definiční obor funkce y= 1-logx (celý výraz je pod odmocninou)
Děkuju moc
Offline
#44 04. 06. 2009 16:11
Re: Příjmačky na VŠE
↑ kubistation:
iˇ2 = -1
iˇ3 = -i
iˇ4 = 1
iˇ5 = iˇ1
výsledek tedy je 1 - i - 1 + i - 1 - i = -1 -i (-1 -1*i)
Offline
#45 04. 06. 2009 16:14
Re: Příjmačky na VŠE
↑ kubistation:
když je výraz pod odmocninou musí být vetší než nula ... záporná odmocnina neexistuje ...
stačí tedy položit část pod odmocninou
1 - log x > 0 ... snad by to mohlo vyjít :D
a pak bych pokračovala podle toho jak vypadá výsledek :D
Offline
#47 04. 06. 2009 16:50
- kubistation
- Zelenáč
- Příspěvky: 21
- Reputace: 0
Re: Příjmačky na VŠE
Děkuju už chápu,akorát def. obor je teda (0,10]? , nula tam bejt nemůže a záporný číslo taky ne, že jo?:)
Offline
#48 05. 06. 2009 02:01
Re: Příjmačky na VŠE
↑ kubistation:
ano další podmínkou je x>0, na tu jsem zapomněla, takže 
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#50 05. 06. 2012 17:11
Re: Příjmačky na VŠE
↑↑ musixx:
Není to bez nulového bodu 3
Tudíž by to mělo být
Pokud se pletu, omlouvám se.
Offline
 .
.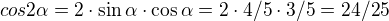
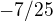

 ?
?