Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 09. 2016 14:14
Předpis funkce
Prosím,
mohl by mi někdo napsat předpis takovéto (podobné) funkce (viz obrázek).
Chci si nakreslit podobný graf :-) 
Fyzika a matematika konečně srozumitelně - www.nabla.cz
Fyzikální bludy
Řešení státní maturity z matematiky
Kdy psát mě a mně
Offline
#2 27. 09. 2016 15:47 — Editoval Rumburak (27. 09. 2016 15:50)
Re: Předpis funkce
Ahoj.
Hledáme fuinkci  takovou, aby zakreslená křivka měla přibližně předpis
takovou, aby zakreslená křivka měla přibližně předpis 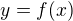 .
.
Zdá se, že jde o křivku symetrickou podle jistého středu ![kopírovat do textarea $S[m,n]$](/mathtex/35/351eac6911e7a00a1dee8ef3b4662c54.gif) . Situaci zjednodušíme, když křivku
. Situaci zjednodušíme, když křivku
posuneme tak, aby měla střed v počátku soustavy souřadnic - příslušnou funkci označme  . Hledaná
. Hledaná
fuinkce  pak bude mít tvar
pak bude mít tvar
 .
.
Funkce  bude zřejmě lichá. Jejím zderivováním obdržíme sudou funkci
bude zřejmě lichá. Jejím zderivováním obdržíme sudou funkci  , která bude na jistém intervalu
, která bude na jistém intervalu
 konstantní s hodnotou
konstantní s hodnotou  . Další už můžeme jen odhadovat, např. volbou
. Další už můžeme jen odhadovat, např. volbou
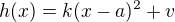 pro
pro  ,
,
 pro
pro 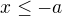 ,
,
kde rovněž  . Pak bude
. Pak bude  .
.
Čísla  volíme tak, aby bylo dosaženo co nejlepšího výsledku.
volíme tak, aby bylo dosaženo co nejlepšího výsledku.
Offline
#3 27. 09. 2016 16:13
Re: Předpis funkce
↑ Rumburak:
Díky.
Fyzika a matematika konečně srozumitelně - www.nabla.cz
Fyzikální bludy
Řešení státní maturity z matematiky
Kdy psát mě a mně
Offline