Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Kde zmizne dx2 (dx na druhú) pri derivácii funkcie x2 (x na druhú). (TOTO TÉMA JE VYŘEŠENÉ)
#26 05. 06. 2009 10:03
Re: Kde zmizne dx2 (dx na druhú) pri derivácii funkcie x2 (x na druhú).
↑↑ kaja(z_hajovny):
Kouknou se na http: durko.blog.sme.sk a budou moudřejší, vo něco.
Skutočnosť, že o túto diskusiu je nedpriemerný záujem, svedčí o tom že matematika ešte nestačila zablokovať slobodnú mysľ študujúcim občanom. Svojim príspevkom, ktorý ale nemá nič spoločného s témou, vyraciaš to čo povrdzuješ.
Offline
#27 05. 06. 2009 10:38
Re: Kde zmizne dx2 (dx na druhú) pri derivácii funkcie x2 (x na druhú).
↑ genius:
Ani by som netvrdil, že tu je nadpriemerný záujem, len tie tvoje reakcie sú tak nevhodné, že treba reagovať. Nepíš sem veľa príspevkov, svoje reakcie na viacerých môžeš zhrnúť aj do jedného príspevku:
↑ genius:
bla bla bla
↑↑ kaja(z_hajovny):
bla bla bla
↑↑ CzechMan:
bla bla bla
Nevypisuj všade ten svoj blog. Myslím, že ti skôr ide o zvýšenie karmy tvojich článkov na sme.sk, pretože aj tak predpokladám je dosť nízka. Ale inak pekný pokus. Ja som si teda na to neklikol a ani nemám záujem. To je môj posledný príspevok na tvoju adresu a pripájam sa k názoru ↑↑ kaja(z_hajovny):. Prosím moderátora o uzatvorenie tejto diskusie.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#28 05. 06. 2009 11:35
Re: Kde zmizne dx2 (dx na druhú) pri derivácii funkcie x2 (x na druhú).
↑ lukaszh:
Ako matematikovi ušla ti jedna maličkosť a to, že tu sa diskutuje o tom, kam sa podela hodnota dx2 z rovnice derivácie funkcie x2. Či by nebolo potrebné to nahlásiť na políciu. Pokiaľ viem tento server je o matematike a nie o kádrovaní účastníkov servra z tvojho osobného zorného uhla. Zapamätaj si, že každý génius pozná svoje kvality, nie je preto zvedavý na hodnotenie negénia. Bol by som ti vďačný keby si sa venoval Teilorovým radom a nie tejto téme.
Offline
#29 05. 06. 2009 11:44
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Kde zmizne dx2 (dx na druhú) pri derivácii funkcie x2 (x na druhú).
Myslím, že nemá smysl to tu dále rozebírat, je přece jasné, že 2 v exponentu x^2 nemá materiální rozměr. A bez toho to těžko použijeme v praxi, tak proč vůbec řešit, jak se to derivuje.
Někdo se trochu pobavil, ale už to začíná být otravné. Sám genius psal, že by si z vyloučení z fóra nic nedělal, mě by to také vůbec nevadilo. Je tu někdo komu ano? Pokud ne, pak není důvod, proč ho nevyloučit.
Offline
#31 05. 06. 2009 12:14
Re: Kde zmizne dx2 (dx na druhú) pri derivácii funkcie x2 (x na druhú).
↑ BrozekP:
Ak by sa hodnota dx2 nevyhodila svojvoľne z rovnice, tak by výsledkom derivácie nebola hodnota 2x, ale 2x +dx. A itegrácia by nemala hodnotu x2, ale x2 +x. Potom by sa mohla podať žaloba na učiteľov matematiky za úmyselný podvod pri odvodzovaní hodnoty derivácie funkcii. Ale v pohode, prejdi na iný server, či ľachšiu tému. Túto tému nastolil génius, tak sa stým dobrovoľne zmier. Tvoje vedomosti z matematiky nelasifikujem, lebo nato nemám právo.
Offline
#32 05. 06. 2009 12:20
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Kde zmizne dx2 (dx na druhú) pri derivácii funkcie x2 (x na druhú).
Jak může učitel úmyslně klamat, když o tom neví? Možná bychom neměli řešit matematické znalosti, ale pouhopouhé uvažování.
To už je druhá žaloba za poslední dva dny. Jestli tohle není recese, tak požíváš asi nějaké hodně silné látky.
Offline
#34 05. 06. 2009 13:33
Re: Kde zmizne dx2 (dx na druhú) pri derivácii funkcie x2 (x na druhú).
↑ halogan:
Priateľu, zver sa všetkým na tomto servriy čo ti, (okrem neznalosti aparátu odvodzovania prvej derivácie funkcii) bráni vyjadrť sa k jedinéj téme tejto diskusie, a to, prečo z predmetnéj rovnice zmyzla hodnota dx2, o nič viac neide. Uvidíš že spoločne sa nám podarí odstrániť tú prkážku, ktorá ti neumožňuje vyjadrovať sa k meritu veci. Medzi tým sa môžeš vdelávať na dnú tému na http: durko.blog.sme.sk. Dôveruj géniovi, chce len a len tvoje dobro.
Offline
#35 05. 06. 2009 14:18 — Editoval rughar (05. 06. 2009 14:33)
Re: Kde zmizne dx2 (dx na druhú) pri derivácii funkcie x2 (x na druhú).
↑↑ genius:
Nemám rád přilévání oleje do ohně. Ale tohle je fakt sila:D
Co krok, to matematický blud člověče. Tak předně něco k limitám
Ta rovnost popřít bohužel nejde. Takže 2x + dx je rovno 2x prostě.
Potom něco k integrálům. Integrál z dx není x.
když mám  , respektive
, respektive  , tak po zintegrování dostanu
, tak po zintegrování dostanu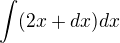 respektive
respektive 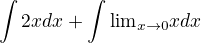
a při vyintegrování mám tedy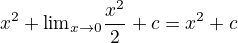
Mimochodem. Integrace není opačná operace k derivování. Liší se. Když něco zderivuješ a pak zintegruješ, nedostaneš totéž! Nic mi neříká proč by to tak mělo nutně být. Integrál i derivace nejsou nerozlučně spojeny. Možná platí že když něco zintegruju a pak zderivuju, tak dostanu totéž. Opačně to ale neplatí. Řešení se liší o konstantní funkci.
Za další "praktické násobení nulou". Aby něco fungovalo prakticky, mělo by to v matematicke fungovat nejprve teoreticky (to je prostě nutný první krok). Násobení funguje na čísla. Takže abys násobení nulou chápal prakticky, musíš ho i v praxi aplikovat na čísla. To jsou počty kuřat v kurníku nebo počet kilometrů ve vzdálenosti, nebo počet litrů v objemu apod. Najsou to kuřata, kilometry ani litry. Jsou to jejich počty. To jsou čísla a a na nich můžeš násobit. A bez problému i nulou a v praktickém případě.
x^3/3 není jehlan. Tohle je objem jehlanu, který má výšku x se čtvercovou podstavou o velikosti hrany x. Cítíš rozdíl mezi tímto a mezi tím když řeknu že to je prostě jehlan? Nyní co znamená derivovat to podle x? Při derivaci podle x vznikne x^2, což je shodou okolností obsah podstavy toho jehlanu.
Materiální podstata čísel a funkcí je s prominutím blbost. Nejsou podstatou, ale možná tak reprezentací. A to reprezentací některých vlastností. Můžeš mít číslo, které ti reprezentuje hmotnost tělesa v kilogramech (ale nikoli číslo, které je hmotnost). Můžeš mít číslo, které ti reprezentuje počet kuřat (ale to číslo nejsou kuřata). Můžeš vyjít trochu dál a místo čísel použít k popisu funkcí. Tvar trajektorie hozeného předmětu může mít tvar paraboly (ale pozor!, hozený předmět není parabola). Přesně takhle se odráží matematika v praxi. Že něco popisuje podle určitých pravidel, které je potřeba znát.
Vím, že matamatika není v mnoha ohledech intuitivní a dělá lidem problémy se ji na začátku naučit a vše pochopit. Z těžkého se však stane nemožné, když budeš ignorovat to co ti druzí lidé, kteří matematiku mají buď vystudovanou a nebo ji studují, budou radit.
Tento server slouží (alespoň si tí já myslím, pokud jsem správně pochopil jeho pravidla) k tomu, že zde lidé kteří mají problém pochopit úlohu/teorii k matematice nebo fyzice, se sem příjdou poradit o řešení/přijít si pro vysvětlení. Poradit znamená uvést problém, vyslechnout druhé, zkusit to pochopit a pak si dojsanit čemu kdo nerozumí. Poradit neznamená přesvědčovat bez důkazu o nějakých pohádkách (doporučují založit si blog) a nezaneřáďovat s prominutím trochu úsměvnými názory tento server. Já to tady mám celkem rád a trochu mě začíná štvát, že tady v tom někdo začne dělat nepořádek. Navrhnul bych adminům zamknout všechny tyto diskuse a vyhradit jim prostor v nějaké nové sekci typu "neudělali matematici někde chybu?"
1 + 1 = 1 + 1
... a nebo taky ne
Offline
#36 05. 06. 2009 14:21
Re: Kde zmizne dx2 (dx na druhú) pri derivácii funkcie x2 (x na druhú).
↑ rughar:
Pozor na ty limitní přechody, máš tam alfu místo proměnné x.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#38 05. 06. 2009 14:28
Re: Kde zmizne dx2 (dx na druhú) pri derivácii funkcie x2 (x na druhú).
↑ rughar:
A stále není, tu první limitu más stále pro  :-)
:-)
Offline
#39 05. 06. 2009 14:45
Re: Kde zmizne dx2 (dx na druhú) pri derivácii funkcie x2 (x na druhú).
↑ rughar:
Tu sa huvorí o derivovaní funkcie x2 a v tomto prípade platí čo tvrdím ja. Otázka stojí naďalej tak: prečo dx2 sa odstraňuje pri derivácii funkcii x2. Ja viem o čom hovorím a preto nepotrebujem citácie z kních, ale iba zo svojho rozumu. Keby ti dal učiteľ jenú neformálnú otázku z derivácii funkcii asi by si mu odpovedal tak ako mne, teda mimo podstaty veci. Vážne pozrí sa na http:durko.bog.sme.sk dozvieš sa viac. Tu na to niet miesta.
Offline
#40 05. 06. 2009 14:52
Re: Kde zmizne dx2 (dx na druhú) pri derivácii funkcie x2 (x na druhú).
↑ genius:
Tady (už sem to psal). (Uvedu odpověď proč platí, že 2x + dx = 2x, je to tvezení které říká totéž co teď ty)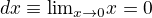
A tedy 2x + 0 = 2x. Souhlasíš alespoň s tímto?
1 + 1 = 1 + 1
... a nebo taky ne
Offline
#41 05. 06. 2009 15:01
Re: Kde zmizne dx2 (dx na druhú) pri derivácii funkcie x2 (x na druhú).
↑ rughar:
Vzácný priateľu, milovník falošnéj mateatiky, keby dx = 0, potom by platilo že aj dy = 0 , no ale potom by každá jedná derivácia bola hodnotou podielu 0/0. V tom prípade by vznikla takzvaná unifikovaná matematika v ktoréj všteky výsledky by boli čisto nulové. Tu sa ukazuje, že ani jeden vyokoškolák namá ani šajnu o hodnote dx, teda o číselnej, nie o filozofickéj hodnote. To však nie je ich chyba. Chyba je v tom, že to nevedia ani ích učitelia. To na svete viem iba ja genius a chcem vám to povedať aby ste neprepadli z matematiky, ale vy ma nechcete počúvať vy sa sažíte ma iba zosmiešniť. Je vôbec možné génia zosmiešniť?
Offline
#42 05. 06. 2009 15:07
Re: Kde zmizne dx2 (dx na druhú) pri derivácii funkcie x2 (x na druhú).
↑ genius:
Ne, to není a je to zbytečné. genius se už dávno zesměšnil sám.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#43 05. 06. 2009 15:20
- Lukee

- Administrátor

- Místo: Opava
- Příspěvky: 1863
- Škola: UPOL, Informatika
- Pozice: Roznašeč reklamních bannerů
- Web
Re: Kde zmizne dx2 (dx na druhú) pri derivácii funkcie x2 (x na druhú).
↑ genius:
> „(…) milovník falošnéj mateatiky (…)“
Obávám se, že toto fórum je určeno právě pro milovníky falešné matematiky a nezdá se, že by chtěl někdo procitnout do té vaši správné matematiky, z čehož vyplývá, že vaše přítomnost zde na fóru je zbytečná a vzhledem k vaší troloidnosti dokonce nežádoucí. Chcete-li tudíž pokračovat ve svých dialozích, najděte si sofistikovanější fórum, doporučuji zpovednice.cz. Pokud chcete i nadále přispívat do tohoto fóra, budete muset opustit své filosování o matematickém fašismu a zařadit se mezi ty, kteří věří, že 1+1=2. Pokud tak neučiníte a budete zde dále přispívat ve stejném duchu, zablokuji vám na toto fórum přístup.
2+2=4
Offline
#44 05. 06. 2009 15:26 — Editoval rughar (05. 06. 2009 15:28)
Re: Kde zmizne dx2 (dx na druhú) pri derivácii funkcie x2 (x na druhú).
↑ genius:
Ne!
dx/dy není zkrácený zápis pro podíl dvou limit (matematika je hold cizí jazyk a abychom ji rozuměli, musíme si přečíst slovník). Ono platí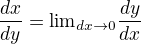
Abychom mohli použít větu o limitě podílu, tedy
musí platit, aby výsledek spodní limity nebyl nula. Tento předpoklad splněný není, nelze tedy dy/dx psát jako podíl limit, ale musíme jej nechat jako limitu celkovou. Uvádíte mě do rozpaků. Nejdřív píšete že tomu rozumíte. Mohu se zpetat čemu? Matematice, kterou lidé považují za matematiku? (tu popíráte). Vlastní matematice? (pak se obávám že sklouzáváte k filozofii, se kterou se nikam nedostaneme). Výše uvednou limitu je potřeba počítat podle pravidel, která jsou shrnuta zde
http://cs.wikipedia.org/wiki/Limitahttp … iki/Limita
A k těm stránkám durko.blog.sme.sk. Každý zákon, třebaže má dobrou myšlenku, má své drobné mezery. Svoboda vyjadřování zdá se není výjimkou. Přečet jsem si článek The Grupa na všem blogu. Kdyby jste znal Newtonovu teorii dobře (ideálně přečet jeho dílo Philosophiae Naturalis Principia Mathematica), tak tam nenajdete žádné zakládání čísel dx,dy,dz a rozhodně nebudete o něm tvrdit, že je hlupák. Kniha je pojmuta hodně o geometrii a teda klobouk dolů před člověkem, který dle mého názoru předběhl pár set let se svými geometrickými poznatky. Mluvení o A. Einstinovi mě zásahlo ještě víc. Na popis svojí teorie (Obecná teorie relativity) použil především Riemannovu geometrii, se kterou byl na začátku problém se zžít. V každém případě jeho dílo je zcela pochopeno a po matematické stránce se mu nedá nic vytknout. A v podstatě to pochopili i před sto lety. Kritikové Einsteinova díla odsuzovali především jeho Speciální teorii, ne však pro její pochopitelnost (když to pochopí 20ti letý student na univerzitě, tak s tím celosvětové kapacity nemají zas takový problém) a srozumitelnost, ale protože nesouhlasili s předpokladem, že světlo se pohybuje konstanntě vůči všem pozorovatelům. Nakonec bylo experimentálně ukázáno že A. Eintein měl pravdu, čímž se popřela teorie o éteru a a teorie relativity byla uznána všemi vědeckými kapacitami za korektní a nejpřesnější, která popisuje gravitaci pro těžké objekty. Dále v článku pokračuje nesouvislé povídání o nějakých diferenciálech a za boha nemohu přijít na to, jak tento výklad diferenciálu koreposnduje s jejich definicí
http://cs.wikipedia.org/wiki/Tot%C3%A1l … nci%C3%A1l
1 + 1 = 1 + 1
... a nebo taky ne
Offline
#46 05. 06. 2009 16:29
Re: Kde zmizne dx2 (dx na druhú) pri derivácii funkcie x2 (x na druhú).
↑ genius:
Už by si mal prestať. Si trapný, tvoje názory sú nevhodné, urážaš matematické kapacity, ktoré niečo o danej problematike vedia, trepeš scesty. Matematika je exaktná veda, neviem čo s týmto chceš docieliť. Ži si vo svojom viacdimenzionálnom harmonickom orechovom svete, ale nezaťažuj s tým okolie. Neviem, čo chceš spochybňovať, pretože už len ten počítač, do ktorého píšeš je dostatočným dôkazom o správnosti matematiky a fyziky. Tvoje orechové výplody ma s prepáčením urážajú.
Prajem stokilometrový orechový koláč, najlepšie šesť dimenzionálny aby si sa z neho najedol. Vytetuj si na čelo dX, dY a dZ, zopakuj si históriu matematiky a prehodnoť svoju definíciu derivácie.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#47 05. 06. 2009 16:43
- Lukee

- Administrátor

- Místo: Opava
- Příspěvky: 1863
- Škola: UPOL, Informatika
- Pozice: Roznašeč reklamních bannerů
- Web
Re: Kde zmizne dx2 (dx na druhú) pri derivácii funkcie x2 (x na druhú).
↑ genius:
„Budte najprv presvedčený na základe exaktných dôkazov a potom sa verejne vyjadrujte“
Dobře.
Je-li někdo majitelem nějakého webového prostoru, pak může rozhodovat o tom, co se tam smí a co nesmí.
Já jsem majitelem tohoto webového prostoru.
Pomocí Modus ponens dostáváme, že já rozhoduji o tom, co se tady smí a co nesmí. A už výše jsem rozhodl, že vaše komentáře v této podobě zde být nesmí. Nezdá se, že byste byl ochoten ustoupit a vylepšit své vystupování, tudíž budete zablokován. Je to dost exaktní? :-)
2+2=4
Offline
#48 05. 06. 2009 16:52
Re: Kde zmizne dx2 (dx na druhú) pri derivácii funkcie x2 (x na druhú).
↑ Lukee:
Ne tejto diskusii záleží budúcnosť ľudstva, preto osobné spory mali by ísť na bok a matematika bymala mať prednosť. Aby história nepísala, že kôli neschopnosti reagovať na exaktné ragumenty genia, ktoré si prečítalo značné množstvo čitateľov, bol genius z diskusie účelne vyradení.
Offline
#49 05. 06. 2009 16:56 — Editoval Rumburak (05. 06. 2009 17:03)
Re: Kde zmizne dx2 (dx na druhú) pri derivácii funkcie x2 (x na druhú).
↑ genius:
Připadá mi, že máš s matematilkou nějaké nevyřízené účty (čemuž se na základě Tvých orientací v matematice ani nedivím), které si zde řešíš.
EDIT: Bez urážky - čím dále sleduji Tvé příspěvky, tím mám silnější dojem, že by ses měl na téma své geniality pobavit s psychiatrem.
Ti pro ni určitě budou mít větší porozumění než nějací matematici.
Offline
#50 05. 06. 2009 16:57
- Lukee

- Administrátor

- Místo: Opava
- Příspěvky: 1863
- Škola: UPOL, Informatika
- Pozice: Roznašeč reklamních bannerů
- Web
Re: Kde zmizne dx2 (dx na druhú) pri derivácii funkcie x2 (x na druhú).
↑ genius:
Já vím, je to smutné. Ale opravdu se zdá, že toto fórum na vás intelektuálně prostě nestačí. Proto jsem vám doporučil jiné fórum, třeba tam budou větší mozky.
2+2=4
Offline
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Kde zmizne dx2 (dx na druhú) pri derivácii funkcie x2 (x na druhú). (TOTO TÉMA JE VYŘEŠENÉ)
