Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 07. 11. 2016 22:27
Problematika čtvercové mříže
Zdravím vás!
(Předem vás varuji, že můj problém je dost rozsáhlá záležitost, bude to na déle.)
Potřebuji dokázat jednu větu, o kterou se pak chci opírat v mé bakalářské práci. Téma práce: Konstruovatelnost objektů ve čtvercové mříži. Intenzivně se tím, co zde budu popisovat, zabývám, napíšu sem všechny střípky, které jsem zatím zjistil.
Def.: Nechť množina C je definovaná takto: 
Věta: Nechť jsou dány dva nesoudělné zlomky  , kde
, kde  . Pak pokud
. Pak pokud  , potom
, potom  .
.
Tak tuhle větu potřebuji dokázat. A teď napíšu, k čemu mi tohle bude.
Mým úkolem je hledat objekty, útvary, které ve čtvercové mříži nelze sestrojit. Čtvercová mříž je síť navzájem kolmých přímek od sebe stejně vzdálených, přičemž každá přímka má, pokud bych si ji představil jako graf fce, sklon rovný 0, anebo nekonečnu (je vodorovná, anebo svislá) a zároveň pro každou dvojici různých přímek p, q platí, že jejich vzdálenost je 1. Při práci s touto mříží mohu používat jen pravítko a pokud chci cokoliv v této mříži sestrojit, musím umět využít strukturu mříže. V takovéto čtvercové mříži se dají některé úsečky dané délky sestrojit, některé zase ne. Pokud pro nějaké přirozené číslo  najdu dvě přirozená čísla
najdu dvě přirozená čísla  , mohu pak sestrojit úsečku délky
, mohu pak sestrojit úsečku délky 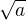 jako přeponu pravoúhlého trojúhelníka, jehož odvěsny jsou právě
jako přeponu pravoúhlého trojúhelníka, jehož odvěsny jsou právě  a
a  . Jsou ale délky, pro něž neexistují odvěsny, a proto jejich odmocniny ASI nemohu sestrojit. Já ještě nevím, záleží na důkazu výše uvedené věty. Například úsečka délky odmocnina ze tří prý sestrojit nejde, a to, že nejde sestrojit, chci nakonec dokázat (rád bych se dostal k něčemu obecnějšímu). Mohl bych to vyřešit Euklidovými větami, ale mohu používat jen pravítko.
. Jsou ale délky, pro něž neexistují odvěsny, a proto jejich odmocniny ASI nemohu sestrojit. Já ještě nevím, záleží na důkazu výše uvedené věty. Například úsečka délky odmocnina ze tří prý sestrojit nejde, a to, že nejde sestrojit, chci nakonec dokázat (rád bych se dostal k něčemu obecnějšímu). Mohl bych to vyřešit Euklidovými větami, ale mohu používat jen pravítko.
--
Co říká tahle věta?
Ta věta říká, že pokud najdu dvě odvěsny  a zároveň součet jejich mocnin bude přirozené číslo, pak pro toto přirozené číslo existují ještě dvě jiné odvěsny, a sice z
a zároveň součet jejich mocnin bude přirozené číslo, pak pro toto přirozené číslo existují ještě dvě jiné odvěsny, a sice z 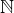 . Speciální případ může nastat, pokud jedna z odvěsen bude rovna nule. Proto číslo
. Speciální případ může nastat, pokud jedna z odvěsen bude rovna nule. Proto číslo  může být v množině
může být v množině  rovno nule. Téhle vlastnosti říkám nepřispívavost zlomků ve čtvercové mříži. Protože pokud se zlomky dají nahradit celočíselnými odvěsnami, nemusím s nimi v mnoha případech pracovat.
rovno nule. Téhle vlastnosti říkám nepřispívavost zlomků ve čtvercové mříži. Protože pokud se zlomky dají nahradit celočíselnými odvěsnami, nemusím s nimi v mnoha případech pracovat.
--
Na co jsem už přišel?
--
1) Vím, že jmenovatele těch dvou zlomků musí být stejné.
Věta: Nechť jsou dány dva nesoudělné zlomky  . Pak
. Pak  , kde
, kde  .
.
Důkaz: SPOREM


Aby  bylo přirozené číslo, muselo by
bylo přirozené číslo, muselo by  být násobkem čísla
být násobkem čísla  .
.
A tedy: 




Pokud  nedělí
nedělí  , pak ani
, pak ani  nedělí
nedělí  (větu, která toto hlásá obecně, jsem dokázal, takže si to můžu dovolit říct).
(větu, která toto hlásá obecně, jsem dokázal, takže si to můžu dovolit říct).
Aspoň v tomhle mám jasno.
--
2) Naprogramoval jsem nějaké funkce a programy, které mi jednak hledají celočíselné dvojice odvěsen pro vstupní přirozené číslo. Vstup: 5, výstup: (1, 2) 
Pak mám jeden rozsáhlejší program, který mi náhodně generuje zlomky se stejnými jmenovateli, umocňuje je a sčítá a pokud je výsledek přirozené číslo, zkontroluje, jestli patří do množiny  . Vygeneroval už přes tisíc různých dvojic zlomků a výsledek (pokud byl přirozený), vždy byl v
. Vygeneroval už přes tisíc různých dvojic zlomků a výsledek (pokud byl přirozený), vždy byl v  . Generoval toho megamoc, ale jen přes tisíc dvojic dalo dohromady přirozené číslo. Z výstupu jsem vykoukal, že jmenovatele ASI mají jednu společnou vlastnost, a sice, že jsou vždy součinem dvou prvočísel, anebo součinem prvočísla a jedničky (ono.... jednička je podle mě speciální prvočíslo, ale podle definice není, takže pokud budu jedničku jako speciální prvočíslo, pak mohu říct domněnku, že jmenovatel je vždy roven součinu dvou prvočísel).
. Generoval toho megamoc, ale jen přes tisíc dvojic dalo dohromady přirozené číslo. Z výstupu jsem vykoukal, že jmenovatele ASI mají jednu společnou vlastnost, a sice, že jsou vždy součinem dvou prvočísel, anebo součinem prvočísla a jedničky (ono.... jednička je podle mě speciální prvočíslo, ale podle definice není, takže pokud budu jedničku jako speciální prvočíslo, pak mohu říct domněnku, že jmenovatel je vždy roven součinu dvou prvočísel).
Předtím jsem si myslel, že jmenovatel samotný bude umocněné prvočíslo minimálně na prvou, jenže pak mi to zbourala dvojice zlomků:

--
Zkoušel jsem všechno možné, ale moje postupy byly takové střípky bez celistvosti, a proto je sem nebudu psát. Už jsem toho napsal až moc, a to proto, abych vám ulehčil práci, pokud mi budete chtít pomoci. Ještě jedna věc: na adrese https://uloz.to/!eiaPVTlun1ug/programy-na-zlomky-rar je rar balíček, ve kterém jsou v Pythonu 3 naprogramovány fce a program pro hledání těch zlomků. V programu pro hledání zlomků se zadává nejdřív dolní mez pro náhodné generování čitatele a jmenovatele a horní mez pro to samé. Pokud můj problém budete řešit, stáhněte si ten balíček. Díky těm konkrétním zlomkům aspoň vím, jak se to chová a díky tomu množství příznivých výsledků tuším, že ta věta platí.
--
Prosím pomozte mi. Budu vám velmi vděčný za každou miniradu.
Není všechno, co se třpytí, není všechno k pochopení.
Není lehké živobytí, a přesto zloba v nás není.
Offline
#2 08. 11. 2016 14:18
- Eratosthenes
- Příspěvky: 2592
- Reputace: 132
Re: Problematika čtvercové mříže
ahoj ↑ Makrofág:,
není mi jasné, co myslíš pojmem "nesoudělné zlomky"...
Budoucnost patří aluminiu.
Offline
#3 08. 11. 2016 15:00
Re: Problematika čtvercové mříže
Ahoj ↑ Eratosthenes:
Zlomek je nesoudělný, pokud neexistuje žádné přirozené číslo větší, než jedna takové, které by dělilo čitatele i jmenovatele. A tím, že říkám nesoudělné zlomky, myslím toto: zlomek  není soudělný
není soudělný 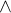 zlomek
zlomek  není soudělný.
není soudělný.
Není všechno, co se třpytí, není všechno k pochopení.
Není lehké živobytí, a přesto zloba v nás není.
Offline
#4 08. 11. 2016 18:01
- Eratosthenes
- Příspěvky: 2592
- Reputace: 132
Re: Problematika čtvercové mříže
ahoj ↑ Makrofág:
zkusil bych přidat ještě tento střípek:
http://docplayer.cz/21417123-Michal-sla … ngles.html
Budoucnost patří aluminiu.
Offline
#5 08. 11. 2016 18:18
Re: Problematika čtvercové mříže
↑ Eratosthenes:
Boží! Díky! Zkusím z toho něco vytřískat :)
Není všechno, co se třpytí, není všechno k pochopení.
Není lehké živobytí, a přesto zloba v nás není.
Offline
#6 08. 11. 2016 18:21
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: Problematika čtvercové mříže
↑ Makrofág:
Ahoj, mně připadá, že tu konstruovatelnost máš definovánu jako právě všechna čísla z množiny C (tj. jako přeponu trojúhelníku, jehož odvěsny jsou celočíselné), tak nevidím, jak s tím souvisí to, že ty dva čtverce, které sčítáš, mohou být zlomky. Je to zajímavá věta, ale jak říkám, nevidím tu souvislost s konstruovatelností.
"Máte úhel beta." "No to nemám."
Offline
#7 08. 11. 2016 18:26
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: Problematika čtvercové mříže
↑ Makrofág:
Ahoj ještě jednou, možná špatně vidím, ale ty v té větě nepředpokládáš  , ale jen
, ale jen  (tak mi to připadá z té úpravy na společného jmenovatele). Nebo se pletu?
(tak mi to připadá z té úpravy na společného jmenovatele). Nebo se pletu?
"Máte úhel beta." "No to nemám."
Offline
#8 08. 11. 2016 21:10
Re: Problematika čtvercové mříže
Ahoj ↑ check_drummer:
K první otázce:
Já chci zlomky ze čtvercové mříže touto větou vyloučit jako něco, co té mříži zhlediska konstruovatelnosti těch délek ničím nepřispívá. Pokud výsledek součtu těch čtverců bude přirozené číslo, vždy bude v  a tím pádem najdu i jiné délky odvěsen, celočíselné, s jejichž pomocí sestrojím chtěnou délku. Takže ty zlomky nehrajou žádnou vůdčí roli. Nazývám to nepřispívavost zlomků jako takový pracovní název. A ty se asi ptáš na to, proč do toho tahám i zlomky, když mi stačí celočíselné odvěsny? Právě já nevím, jestli to stačí. Dokázat tu mou větu by pak fakt znamenalo, že to stačí a zlomky pro mě nebudou důležité.
a tím pádem najdu i jiné délky odvěsen, celočíselné, s jejichž pomocí sestrojím chtěnou délku. Takže ty zlomky nehrajou žádnou vůdčí roli. Nazývám to nepřispívavost zlomků jako takový pracovní název. A ty se asi ptáš na to, proč do toho tahám i zlomky, když mi stačí celočíselné odvěsny? Právě já nevím, jestli to stačí. Dokázat tu mou větu by pak fakt znamenalo, že to stačí a zlomky pro mě nebudou důležité.
--
K druhé otázce. Máš pravdu. V důsledku ve znění té věty o různých jmenovatelích jsou umocněné zlomky, ale důkaz pak provádím s neumocněnými.
(odbočka)
Pokud umocním nesoudělný zlomek (viz má definice nesoudělnosti), bude pořád nesoudělný, protože do součinu čitatele a jmenovatele přidávám čísla, která už tam jsou a tím pádem se zase nemá co krátit.
(odbočka)
Na základě tohoto můžu zlomky  a
a  hned v začátku důkazu umocnit, nesoudělnost zůstane a já si je pak označím jen jinými písmeny. A budu pokračovat v důkazu analogicky, jen s jinými písmeny. I tak to dokážu nakonec, to jsem teda rád :)
hned v začátku důkazu umocnit, nesoudělnost zůstane a já si je pak označím jen jinými písmeny. A budu pokračovat v důkazu analogicky, jen s jinými písmeny. I tak to dokážu nakonec, to jsem teda rád :)
Není všechno, co se třpytí, není všechno k pochopení.
Není lehké živobytí, a přesto zloba v nás není.
Offline
#9 10. 11. 2016 14:55 — Editoval check_drummer (10. 11. 2016 15:05)
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: Problematika čtvercové mříže
↑ Makrofág:
Tvá věta se, dle mého, redukuje na důkaz tvrzení, že pro přirozená a,c,n,p, kde nsd(a,n)=nsd(c,n)=nsd(a,c)=1, p je prvočíslo, nemá rovnice  řešení. Je to tak?
řešení. Je to tak?
Edit: špatně jsem si přečetl zadání, úkolem je dokázat, že pomocí zlomků nelze sestrojit více hodnot n než pomocí celých čísel, tak to tvrzení výše není pravda - konečně např. a=3,c=4,n=1,p=5 to vyvrací.
"Máte úhel beta." "No to nemám."
Offline
#10 10. 11. 2016 16:40
Re: Problematika čtvercové mříže
Poznamka.
Iste by sa ti oplatilo podrobne vysetrit cisla ktore su sucet dvoch stvorcov.
Precitaj si aspon
https://fr.m.wikipedia.org/wiki/Théor&# … _de_Fermat
a aj
https://en.m.wikipedia.org/wiki/Fermat% … wo_squares
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 15. 11. 2016 18:42
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: Problematika čtvercové mříže
↑ vanok:
Ahoj, z toho to myslím pěkně plyne - a z toho, že jmenovatelé obou zlomků musí být stejné.
"Máte úhel beta." "No to nemám."
Offline
#12 19. 03. 2017 20:36
Re: Problematika čtvercové mříže
Zdravím vás!
Touha dokázat tu větu mě neopustila, místo té původní věty, kterou jsem nazval jako věta o nepřispívavosti zlomků (dále už jen VNZ), jsem formuloval větu jinou. Tu, když dokážu, nebo společně tady dokážeme, tak dokážeme i větu původní.
Zkoušel jsem všechno možné, až jsem si řekl, že si zkusím analyticky ze všeho, co vím, sestavit něco jednoduššího a uchopitelnějšího. A tak....
Připomenutí: VNZ říká, že když mám daný pravoúhlý trojúhelník se zlomkovými odvěsnami (jejich délky jsou nesoudělné zlomky), kde obsah plochy čtverce nad přeponou je přirozené číslo, pak najdu i celočíselné odvěsny pro tu samou přeponu. To znamená, že na Thaletově kružnici pro přeponu existuje aspoň jeden bod, od kterého je to k oběma krajním bodům přepony celočíselně daleko. Chci dokázat, že na té kružnici aspoň jeden takový bod bude ležet.
Jak jsem na to šel analyticky: (zas tolik jsem toho ale nevymyslel)
Přepona s krajními body  leží na ose
leží na ose  , přičemž
, přičemž 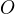 je počátek souřadnic. Zajímá mě bod splňující výše psané.... Hledaný bod B leží na Thaletovce, a tak jsem si odvodil předpis fce pro kladnou Thaletovku nad přeponou:
je počátek souřadnic. Zajímá mě bod splňující výše psané.... Hledaný bod B leží na Thaletovce, a tak jsem si odvodil předpis fce pro kladnou Thaletovku nad přeponou:  , kde
, kde  je obsah plochy čtverce nad přeponou. Bod
je obsah plochy čtverce nad přeponou. Bod  má tedy souřadnice
má tedy souřadnice ![kopírovat do textarea $[x;\sqrt{\sqrt{n}x-x^2}]$](/mathtex/22/225ad7439ce4f8906661659f85f6edc6.gif) . Podobně vektor
. Podobně vektor  Vektor pro druhou odvěsnu
Vektor pro druhou odvěsnu  . Jde mi o délku odvěsen, a tak spočítám obecně jejich délky.
. Jde mi o délku odvěsen, a tak spočítám obecně jejich délky.  ,
,  Bod, který hledám, stačí, aby ležel na levé čtvrtkružnici - vyjádřeno podle jeho x-ové souřadnice, hledám
Bod, který hledám, stačí, aby ležel na levé čtvrtkružnici - vyjádřeno podle jeho x-ové souřadnice, hledám ![kopírovat do textarea $[x;\sqrt{\sqrt{n}x-x^2}]$](/mathtex/22/225ad7439ce4f8906661659f85f6edc6.gif) pro
pro  . Pro obecně vypočtené délky zároveň musí platit, že
. Pro obecně vypočtené délky zároveň musí platit, že  . Chci prostě
. Chci prostě  , která VZNIKNOU ze součtu umocněných zlomků, najít
, která VZNIKNOU ze součtu umocněných zlomků, najít  v daném intervalu čtvrtkružnice tak, aby byly všechny podmínky splněny. Například pro trojku, šestku jsem nenašel řešení a geogebra mi potom ukázala, že řešení fakt neexistuje. (A nemělo by být, protože pro tato čísla neexistují celočíselné odvěsny.) Z toho, co jsem zatím vykousal, mám radost, protože mám aspoň takový dvouvzorečkový návod, jak ty přirozené délky hledat. Lepší, než v listopadu je to.
v daném intervalu čtvrtkružnice tak, aby byly všechny podmínky splněny. Například pro trojku, šestku jsem nenašel řešení a geogebra mi potom ukázala, že řešení fakt neexistuje. (A nemělo by být, protože pro tato čísla neexistují celočíselné odvěsny.) Z toho, co jsem zatím vykousal, mám radost, protože mám aspoň takový dvouvzorečkový návod, jak ty přirozené délky hledat. Lepší, než v listopadu je to.
Prosím pomozte mi s důkazem existence toho kouzelnýho bodu. I kdybychom to nevyřešili, může to zůstat pro někoho jiného, ať se v tom louská. To by mělo taky smysl. Začíná jaro, a tak to dokážem :)
Není všechno, co se třpytí, není všechno k pochopení.
Není lehké živobytí, a přesto zloba v nás není.
Offline
#13 21. 03. 2017 18:11
- check_drummer

- Příspěvky: 4650
- Reputace: 101
Re: Problematika čtvercové mříže
↑ Makrofág:
Ahoj, no já myslím, že jsme ten problém již vyřešili v sychravém podzimu. Ingredience jsou:
1) Odkaz, který dal vanok výše, resp. odkaz, který z té stránky vede:
https://en.m.wikipedia.org/wiki/Sum_of_ … es_theorem
2) Tvrzení, které jsi dokázal, že oba zlomky, jejichž čtverce sčítáš, mají stejný jmenovatel.
Kdyžtak sem přidám časem důkaz, přijde mi snadný.
"Máte úhel beta." "No to nemám."
Offline
#14 16. 10. 2017 16:22
Re: Problematika čtvercové mříže
Díky check_drummerovi.
S využitím věty z odkazu: https://en.m.wikipedia.org/wiki/Sum_of_ … es_theorem
dokážu svou VNZ.
Věta, na kterou bych v životě nepřišel:
Přirozené číslo  větší, než 1 se dá zapsat jako součet mocnin dvou přirozených čísel (má své přirozené odvěsny) právě tehdy, když prvočíselný rozklad
větší, než 1 se dá zapsat jako součet mocnin dvou přirozených čísel (má své přirozené odvěsny) právě tehdy, když prvočíselný rozklad  neobsahuje prvočíslo
neobsahuje prvočíslo  umocněné na lichou mocninu, pro něž platí:
umocněné na lichou mocninu, pro něž platí:
Důkaz VNZ:


Levá strana je součet kvadrátů přirozených čísel, takže ve svém rozkladu neobsahuje naši příšerku, kterou jsme popsali ve větě, na kterou bych v životě nepřišel. Když levá, pak i pravá. Pokud by se v součinu  v prvočíselném rozkladu vyskytovalo to problémové číslo, vyskytovalo by se i v čísle
v prvočíselném rozkladu vyskytovalo to problémové číslo, vyskytovalo by se i v čísle  , což je spor, protože tam není. Nevyskytuje se tedy ani v rozkladu pro
, což je spor, protože tam není. Nevyskytuje se tedy ani v rozkladu pro  , respektive pro
, respektive pro  , ani pro
, ani pro  . Podle věty z odkazu jedna strana ekvivalence říká, že pokud se v rozkladu pro to číslo nevyskytuje naše problémové číslo (pracovně jsem ho nazval příšerka, ikdyž to není matematické), pak pro testované číslo existuje aspoň jedna pythagorejská dvojice. Tudíž existují nějaká
. Podle věty z odkazu jedna strana ekvivalence říká, že pokud se v rozkladu pro to číslo nevyskytuje naše problémové číslo (pracovně jsem ho nazval příšerka, ikdyž to není matematické), pak pro testované číslo existuje aspoň jedna pythagorejská dvojice. Tudíž existují nějaká  a
a  takové, že
takové, že  .
.
--
VNZ tedy říká, že ty odvěsny vždycky najdeme. Druhá otázka, kterou nechám pro čtenáře otevřenou: Jaké jsou způsoby, jak je najít?
Děkuji za rady, za odkazy. Pral jsem se s tím dlouho. A to proto, že jsem se na to snažil přijít úplně sám bez těch odkazů. Nakonec jsem za tu větu o těch rozkladech rád. Bez ní nevím, kde bych skončil. Dokázal jsem to? Jako matematik bych se neměl ptát, ale já se zeptám: Dokázal?
Není všechno, co se třpytí, není všechno k pochopení.
Není lehké živobytí, a přesto zloba v nás není.
Offline
