Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Diskrétna matika - skladanie symetrií šesťuholníka (TOTO TÉMA JE VYŘEŠENÉ)
#1 20. 11. 2016 10:25
Diskrétna matika - skladanie symetrií šesťuholníka
Spontánne mi (v češtine) napadla táto úloha.
Je dán jazyk L = {·} s rovností, kde · je binární funkční symbol. Uvažme jeho realizaci D, kde nosičem je množina
všech symetrií pravidelného šestiúhelníka a · se realizuje jako skládání. (Připomeňme, že
sestává z identity, pěti rotací a šesti osových symetrií.)
Neprišiel som však na to, čo znamená "· se realizuje jako skládání". Binárny funkčný symbol . je typu  , ale čo presne robí? Vezme dva (vo všeobecnosti aj identické) automorfizmy šesťuholníka a aký šesťuholník vráti?
, ale čo presne robí? Vezme dva (vo všeobecnosti aj identické) automorfizmy šesťuholníka a aký šesťuholník vráti?
Ak by mi (spontánne) napadlo pokračovanie úlohy "Zadejte formuli 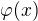 jazyka L takovou...", znamená to, že každá premenná okrem
jazyka L takovou...", znamená to, že každá premenná okrem  musí byť viazaná a
musí byť viazaná a  môže byť aj voľná aj viazaná?
môže byť aj voľná aj viazaná?
Ďakujem za pomoc (so zadaním).
Offline
- (téma jako vyřešené označil(a) Slazer)
#2 20. 11. 2016 11:28
Re: Diskrétna matika - skladanie symetrií šesťuholníka
↑ Slazer:
Ta tečka je obyčejné skládání fcí. Výsledkem je zase automorfismus, ne šestiúhelník.
S tím, jestli x musí mít volný výskyt, to nevím. To je asi třeba podívat se do definice.
What does a drowning number theorist say?
'log log log log ...'
Offline
#3 20. 11. 2016 12:16
Re: Diskrétna matika - skladanie symetrií šesťuholníka
↑ Andrejka3:
Pozrel som si skladanie funkcií, ale stále tomu nerozumiem. Aké funkcie tam skladáme? Môžem poprosiť o konkrétny príklad na  ?
?
Offline
#4 20. 11. 2016 12:30 — Editoval Sherlock (20. 11. 2016 12:41)
Re: Diskrétna matika - skladanie symetrií šesťuholníka
↑ Slazer:
Prvky  chápeme jako permutace (což jsou bijektivní funkce), proto když např. dáš dohromady 2 rotace a 1 symetrii tak se tomu říká skládání (skládáš ty příslušné permutace). Ale to je celkem jedno. Důležitý je tak nějak intuitivně vědět, jak ty prvky vypadají a jak se chovají.
chápeme jako permutace (což jsou bijektivní funkce), proto když např. dáš dohromady 2 rotace a 1 symetrii tak se tomu říká skládání (skládáš ty příslušné permutace). Ale to je celkem jedno. Důležitý je tak nějak intuitivně vědět, jak ty prvky vypadají a jak se chovají.
Tady je např. 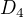 . Obsahuje 1 identitu, 3 rotace a 4 symetrie.
. Obsahuje 1 identitu, 3 rotace a 4 symetrie.
čtverec v původní poloze si označme 
čtverec "rotate 90 degrees" reprezentuje otočení o 90 stupňů. pokud si toto otočení označíme třeba jako  , bude platit že
, bude platit že 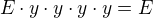 (pokud čtyřikrát otočíš čtverec o 90, dostaneš ho ve stejné poloze)
(pokud čtyřikrát otočíš čtverec o 90, dostaneš ho ve stejné poloze)
toto samozřejmě neplatí jen pro  , pokud libovolný čtverec z těchto osmi 4x otočíš o 90 stupňů, dostaneš ten, který jsi měl na začátku :)
, pokud libovolný čtverec z těchto osmi 4x otočíš o 90 stupňů, dostaneš ten, který jsi měl na začátku :)
Offline
#5 20. 11. 2016 13:21
Re: Diskrétna matika - skladanie symetrií šesťuholníka
↑ Slazer:
Když si označím vrcholy 6-úhelníku jako 1,2,3,4,5,6, pak zrcadlení (či osová souměrnost) podle uhlopříčky 1,4 je fce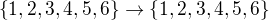 , označme ji
, označme ji  , která funguje takhle:
, která funguje takhle: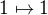 ,
, 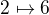 ,
,  , atd.
, atd.
Pak f složena sama se sebou je zase fce 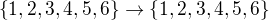 . Obraz dvojky fce
. Obraz dvojky fce 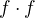 je pak
je pak 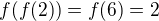 .
.
What does a drowning number theorist say?
'log log log log ...'
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Diskrétna matika - skladanie symetrií šesťuholníka (TOTO TÉMA JE VYŘEŠENÉ)
