Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 29. 11. 2016 22:49
Re: Dokázání ekvivalence s derivací
↑ Andrejka3: Nejsou. V zadání je akorát napsáno, že mám ukázat, že ekvivalence platí.
Offline
#5 29. 11. 2016 22:59 — Editoval Andrejka3 (29. 11. 2016 23:01)
Re: Dokázání ekvivalence s derivací
↑ 142957:
Zkusme začít implikací zprava doleva.
Můžeme předpokládat, že
(1) 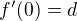 pro jisté pevné
pro jisté pevné 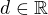 ,
,
(2) platí předpoklad implikace vlevo, tj.  konverguje.
konverguje.
(1) můžeme rozepsat jako limitu. Z (2) a nutné podmínky konvergence plyne další limita...
Tuším, že to jde k cíli.
edit: to by jen vedlo k důkazu, že f (a_n) konverguje, ale o sume to nic nerekne.. viz jarrro.
What does a drowning number theorist say?
'log log log log ...'
Offline


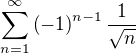 konverguje ale
konverguje ale 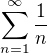 diverguje
diverguje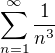 vs.
vs. má deriváciu v nule ale nezachováva konvergenciu.
má deriváciu v nule ale nezachováva konvergenciu.