Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita posloupnosti (TOTO TÉMA JE VYŘEŠENÉ)
#1 06. 12. 2016 12:20 — Editoval dominiksep (06. 12. 2016 12:24)
- dominiksep
- Příspěvky: 54
- Reputace: 0
Limita posloupnosti
Ahoj,
potřebuji pomoct s následující limitou posloupností:![$\lim_{n\to + \infty } \sqrt[n]{3^n+n-5}$](/mathtex/03/03ed51eb6bbdb618a545ba2c71d47ef1.gif "kopírovat do textarea")
Už jsem zkoušel Cauchyovu větu a podílové kritérium.
Děkuji
Offline
- (téma jako vyřešené označil(a) dominiksep)
#2 06. 12. 2016 12:42
Re: Limita posloupnosti
↑ dominiksep:
Ahoj.
Zkus hledat vhodné odhady zdola a shora. Nabízí se
![$\sqrt[n]{3^n} < \sqrt[n]{3^n+n-5} < \sqrt[n]{3^n+3^n}$](/mathtex/a7/a7b53e88a28a46c6e3a9a35266ad27a7.gif "kopírovat do textarea")
pro dostatečně velká 
.
Offline
#3 06. 12. 2016 16:40 — Editoval Pritt (06. 12. 2016 16:40)
.
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita posloupnosti (TOTO TÉMA JE VYŘEŠENÉ)
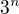