Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Pozdní Medardův polynom (TOTO TÉMA JE VYŘEŠENÉ)
#2 08. 06. 2009 16:31 — Editoval Pavel (08. 06. 2009 16:31)
Re: Pozdní Medardův polynom
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Pozdní Medardův polynom (TOTO TÉMA JE VYŘEŠENÉ)

![kopírovat do textarea $P(x)\in\mathbb{R}^+[x]$](/mathtex/e7/e72dd44191ee0ea440c3fe522396c4cb.gif) je polynom (s kladnými koeficienty). Dokažte, že jestliže platí pro x=1 nerovnost
je polynom (s kladnými koeficienty). Dokažte, že jestliže platí pro x=1 nerovnost
 . Pak
. Pak  platí, že
platí, že
 pro
pro  .
.  a pro libovolné
a pro libovolné 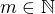 platí
platí
 , platí, že
, platí, že
