Matematické Fórum

lukelee36 · 23. 01. 2017 15:21

Zdravím, pořeboval bych poradit s příkladem, nevím si s ním rady.

Nalezněte Taylorův rozvoj funkce f v bodě x0 a určete obor (stejnosměrné) konvergence, je-li:
$f(x)=\sqrt[3]{(1+x)^{2}}$
$x_{0}=0$

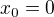
Děkuji za odpovědi

Freedy · 23. 01. 2017 15:43 — Editoval Freedy (23. 01. 2017 22:59)

ahoj,

zkus si dokázat následující vztah
$T^n_{(1+x)^r, 0}=1+ {r \choose 1}x + {r \choose 2}x^2 + ... + {r \choose n}x^n + o(x^{n})$
potom už bude tvůj příklad pouze speciálním případem.

(PS: je to kdyžtak stejnoměrná, nikoliv stejnosměrná konvergence)

lukelee36 · 23. 01. 2017 15:47

↑ Freedy:
Kouknu na to.

To jsem se přehlédl, elektrikář se ve mě nezapře..

lukelee36

Chápu to správně ?
$(1+x)^r=1+rx+\frac{r(r-1)}{2}x^{2}+\frac{r(r-1)(r-2)}{3!}x^{3}+...$

Jj · 23. 01. 2017 16:56

↑ lukelee36:

Zdravím.

Ano, je to tak.

Al1 · 23. 01. 2017 18:03

↑ lukelee36:

Zdravím,

dokonce to chápeš správně. :-)

lukelee36

Trochu tedka nevím co dál.
Vzhledem že aritmetickou úpravou si můžu zápis funkce upravit na:
$\sqrt[3]{(1+x)^{2}}=(1+x)^{\frac{2}{3}}$
Tak by to podle mě mělo jít jenom dosadit za r. Ale teď už mi hlava nebere, jak to rozvinout$.

Freedy · 24. 01. 2017 01:31

↑ lukelee36: vždyť pouze dosadíš za r ;)

Matematické Fórum

#1 23. 01. 2017 15:21

Taylorův rozvoj funkce f

#2 23. 01. 2017 15:43 — Editoval Freedy (23. 01. 2017 22:59)

Re: Taylorův rozvoj funkce f

#3 23. 01. 2017 15:47

Re: Taylorův rozvoj funkce f

#4 23. 01. 2017 16:50 — Editoval lukelee36 (23. 01. 2017 22:28)

Re: Taylorův rozvoj funkce f

#5 23. 01. 2017 16:56

Re: Taylorův rozvoj funkce f

#6 23. 01. 2017 18:03

Re: Taylorův rozvoj funkce f

#7 24. 01. 2017 00:34 — Editoval lukelee36 (24. 01. 2017 00:34)

Re: Taylorův rozvoj funkce f

#8 24. 01. 2017 01:31

Re: Taylorův rozvoj funkce f

Zápatí