Matematické Fórum

aferon · 23. 01. 2017 19:57

Ahoj, mohl by mi někdo poradit jak najdu extrémy funkce vzhledem k množině a hranici? pomocí Lagrangea? Děkuji.
//forum.matweb.cz/upload3/img/2017-01/97824_V%25C3%25BDst%25C5%2599i%25C5%25BEek.JPG

Rumburak

↑ aferon:
Ahoj.

Metoda Lagrangeova multiplikátoru zde nebude potřeba.
Množina $V$ je uzavřená v 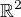$\mathbb{R}^2$ , její hranici $\partial V$ je přímka o rovnici $y = 0$ , tj. osa $x$ .

Extrémy funkce $f$ vzhledem k $\partial V$ budou odpovídat extrémům funkce $g(x) := f(x, 0)$
jedné reálné proměnné.

K určení extrémů funkce $f$ ve vnitřních bodech množiny $V$ se použije standardní postup
(přes "podezřelé" body, v nichž parciální derivace fce $f$ jsou rovny 0 nebo některá z nich
neexistuje).

aferon · 24. 01. 2017 11:19

↑ Rumburak:
Děkuji za odpověď. Bohužel ve zkouškových písemkách po nás chtějí použít právě Lagrangea. Nikde jsem na to nenašel nějaký vyřešený příklad. Ve škole jsme spočítali jeden. Neměl byste na to nějaké materiály? Děkuji.

Rumburak · 24. 01. 2017 11:49

↑ aferon:

Toto téma je vyloženo v knize Vojtěch Jarník: Diferenciální počet II. ,
která navíc je (nebo aspoň donedávna byla) publikována i na webu.

aferon · 25. 01. 2017 09:44

↑ Rumburak:
Děkuji za užitečný materiál. Mohl bych se ještě zeptat, jaký je rozdíl v extrémech funkce vzhledem k hranici a vzhledem k množině? Děkuji.

Rumburak · 25. 01. 2017 13:59

↑ aferon:

Základním pojmem je obecný pojem extrému funkce $f$ vzhledem k množině $M$ ,
která je částí definičího oboru 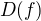$D(f)$ funkce $f$ . Pokud i hranice $\partial M$ množiny $M$
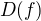je částí $D(f)$ , můžeme hledat extrémy funkce $f$ vzhledem k $\partial M$ .
Pojmově v tom tedy žádný rozdíl není, $\partial M$ je obecně jen jiná množina než $M$ .
Obě úlohy se ovšem (v typických úlohách) liší metodami řešení, tj. extrémy vzhledem
k otevřenému kruhu se hledají jinak než extrémy vzhledem k jeho obvodové kružnici.
V prvém případě hovoříme o jednoduchých extrémech a hledáme je mezi těmi body kruhu,
v nichž PD neexistují nebo jsou obě nulové. Ve druhém případě jde o extrémy s vazbou
a zde se může hodit věta o Lagrangeově multiplikátoru, pokud funkce splňuje předpoklady
příslušné věty.

aferon · 25. 01. 2017 16:07

↑ Rumburak:
Děkuji za odpověď. Příklad vyřeším a přidám sem příspěvek s výpočty.

aferon · 25. 01. 2017 19:10 — Editoval aferon (25. 01. 2017 20:36)

↑ Rumburak:
Ještě se chci zeptat k tomu úkolu b). Píšete, že jednoduché extrémy uvnitř množiny, jsou takové extrémy, kde je PD rovna nule, či neexistuje. Čili pomocí tohoto kroku najdu tedy jen podezdřelé body? viz. obr. A jak určím který z nich je extrém? Budu potřebovat druhé parciální derivace?
K tomu bodu a) dočetl jsem se, že metodu Lagrangeových multiplikátorů je možno použít pouze pro hledání vázáných extrémů na kompaktních množinách. Nezdá se mi, že by množina y<=0 byla kompaktní. Zřejmě mi stále něco uniká. Děkuji.
//forum.matweb.cz/upload3/img/2017-01/72714_V%25C3%25BDst%25C5%2599i%25C5%25BEek.JPG

Rumburak

↑ aferon:

K extrémům ve vnitřních bodech:
Ano, uvedenou metodou lze zjistit podezřelé body. K ověření, zda v takovém bodě
skutečně jde o lokální extrém, nutno analysovat chování funkce v jeho okolí. Druhé
derivace mohou při tomto vyšetřování pomoci, ale není to tak mechanické jako u funkcí
jedné proměnné. Své místo zde má tzv. Hessův determinant, pokud se nemýlím v názvu.

K extrémům na hranici množiny:
Věta o L.m. také dává (za příslušných předpokladů) jen nutnou podmínku, takže body,
které ji splní, jsou jen mezi podezřelými (zda existují i další podezřelé body, závisí
na množině a na funkci).

Kompaktností "celé" množiny je při spojitosti
vyšetřované funkce zaručeno, že:

1. existují její absotutní extrémy přes celou množinu,
2. existují její absotutní extrémy podél hranice množiny (protože i tato hranice je
za uvedenách předpokladů kompaktní množinou).

V praxi to znamená, že mezi podezřelými body určitě jsou ty, v nichž
je dosaženo abs. extrémů, takže pak stačí jen porovnat funkční hodnoty
v podezřelých bodech.

PS. Nevím, co je obrázek A.

Pokud jde o polorovinu $x \le 0$ , tak její hranicí je přímka $x = 0$ ,
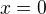což lze vnímat jako vazební podmínku pro větu o L.m.
Pokud v nějakém jejím bodě bude podmínka z této věty splněna, potom
daný bod můžeme prohlásti za podezřelý.
A naopak: když v nějakém bodě této přímky bude mít funkce lok. extrém
vzhledem k této přímce a budou-li v něm splněny předpoklady věty o L.m.,
pak ho tato věta odhalí.

aferon · 28. 01. 2017 00:17 — Editoval aferon (28. 01. 2017 00:22)

↑ Rumburak:
Děkuji za odpověď. Vypočítal jsem to zadání. Mohl bych Vás poprosit zda byste se na to v rychlosti nepodíval? Nevím, jak si mám vyložit výsledek bodu bodu P vzhledem k hranici? Čili funkce f má vázané maximum = 5 v bodě P[0;0] ?
Děkuji.
Edit: a=0 je špatně; místo toho $\lambda =-8$
//forum.matweb.cz/upload3/img/2017-01/59004_V%25C3%25BDst%25C5%2599i%25C5%25BEek1.JPG

aferon · 29. 01. 2017 21:45 — Editoval aferon (29. 01. 2017 22:27)

↑ Rumburak:
ještě bych se chtěl zeptat, jaký je rozdíl mezi vázaným extrémem a vázaným lokálním extrémem? Našel jsem totiž publikaci na internetu, kde se zabývají vázanými lokálními extrémy a řeší tam příklady typu viz. obr. Dala by se ta podmínka, která je tam uvedena brát jako hranice?

Trochu mě zmátlo, že v té publikaci určují extrémy pomocí výsledku determinantu, měl jsem za to, že stačí vypočíst podezdřelé body z extrému a dosadit je do funkce a zjistit jejich funkční hodnoty a dle toho rozhodnout o jaký extrém se jedná.

Dále se chci zeptat, je tam uvedeno, že pokud Lagran. funkce nemá v bodech extrém, tak to neznamená, že samotná funkce nemá extrém a pak přijde na řadu tato věta //forum.matweb.cz/upload3/img/2017-01/25054_V%25C3%25BDst%25C5%2599i%25C5%25BEekdd.JPG . Je užitečná i pro tento příklad?

Děkuji.

odkaz na publikaci: http://homen.vsb.cz/~kre40/esfmat2/kapi … la_6_2.pdf

Rumburak

↑ aferon:

Minulý týden jsem byl mimo web, ale nyní můžeme případně pokračovat, pokud je
něco z tématu ještě aktuální.

Prozatím doporučují umět se na úlohu podívat také geomtricky .
Spojitou reálnou funkci $f$ dvou reálných proměnných definovanou na oblasti $G$
si můžeme představit jako plastickou mapu krajiny, při čemž $f(x,y)$ značí nadmořskou
výšku "prostorového" bodu $[x, y, f(x,y)]$ (zatímco $[x, y]$ je "rovinný" bod půdorysu
naší plastické mapy, v němž je dána kartéská soustava souřadnic Pxy a oblast $G$ ).
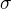Rovnicí $z = f(x,y)$ je pak popsána jistá plocha $\sigma$ nad oblastí $G$ .

Předpokládejme, že

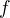(1) v "rovinném" bodě $A = [a, b]\in G$ je lokální maximum fce $f$ vzhledem ke $G$ .

Podle definice lok. maxima to znamená, že v rovině $Pxy$ existuje okolí $U$ bodu $A$
takové, že pro každé $X \in U$ je $f(X) \le f(A)$ . (Pro ostré lokální maximum by
i poslední nerovnost byla ostrá.)

To znamená, že "prostorový" bod $[A, f(A)]$ "je vrcholem (nějaké) hory" (v případě
ostrého maxima) nebo případně "leží na nějakém hřebenu či plošině" a pod. (připouštíme-li
i neostré maximum).

Bodem $[A, f(A)]$ prochází jednak plocha 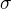$\sigma$ , jednak rovina $\varrho$ o rovnici $z = f(A)$ .
Z předpokladu (1) plyne, že rovina $\varrho$ je v bodě $[A, f(A)]$ opěrnou rovinou plochy $\sigma$ .
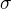V případě hladké plochy 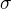$\sigma$ , tj. hladké funkce $f$ , tedy jde o tečnou rovinu a odtud nutné
podmínky

$\frac{\partial f}{\partial x} (A) = \frac{\partial f}{\partial y} (A) = 0$ .

Příště se můžeme podívat tímto způsobem na extrémy vzhledem k rovinné křivce,
bude-li zájem. Nyní ale musím končit.