Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#5 27. 01. 2017 15:02 — Editoval vanok (27. 01. 2017 19:52)
Re: limita
↑ Elisa:,
Ahoj,
Preco nepouzijes taylorov rozvoj okolo nuly.
A tak 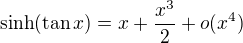
A urobis rozvoj pre tvoj vyraz .... uvidis, vdaka tomu, ze limita je 
Edit. Preklep opraveny. Dakujem za upozornie kolegom Al1.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 27. 01. 2017 20:04 — Editoval vanok (27. 01. 2017 22:03)
Re: limita
↑ Elisa:,
Vies ako robit rozvoje zlozenych funkcii?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 28. 01. 2017 10:25 — Editoval vanok (28. 01. 2017 10:36)
Re: limita
Schematicky
Tu staci vediet, ze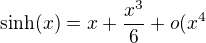
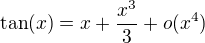
( vies, ze 3!=6, akoze nam staci urobit rozvoj do radu 4, netreba ist dalej)
Dosadenim mas, ( akoze pracujes v rade 4, mas pravo zabudnut na vsetko co da mocninu vädciu ako 4)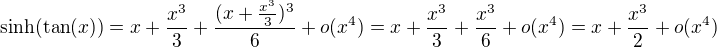
A tak 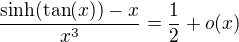
Na cviceniach by ste mali porobit plno takychto vypoctov, ( je to o mnoho dolezitejsie vediet ako sa trapit bez prestania napr z r.H...)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 30. 01. 2017 21:04
Re: limita
Ahoj ↑ Marian:,
Este sa vyhodne da pouzit napr. metodu ekvivalentov (a su aj ine), ale ako sa zda, podla toho co mi tu pisali vlani viaceri foristi, to sa v cz a ani na sk neuci. (To je podla mna skoda, ale preco by som mal niekoho na silu nieco ucit)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline




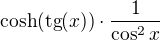 . To ale musíš derivovat jako součin. A derivace
. To ale musíš derivovat jako součin. A derivace  je 6x (pokud si již nějak nepokrátila)
je 6x (pokud si již nějak nepokrátila)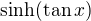 je ovšem jiný, než napsal kolega vanok, asi jen překlep ve jmenovateli zlomku.
je ovšem jiný, než napsal kolega vanok, asi jen překlep ve jmenovateli zlomku.