Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » Funkce s parametrem (TOTO TÉMA JE VYŘEŠENÉ)
#1 06. 02. 2017 19:58 — Editoval Marian (20. 02. 2017 20:22)
Funkce s parametrem
Předpokládám, že pro olympiádní nadšence ze SŠ bude tato úloha zábavná a možná i překvapující. Ochutnejte matematický zákusek...
Je dána funkce  proměnné
proměnné  předpisem
předpisem
a) Dokažte, že je tato funkce konstantní vzhledem k proměnné z.
b) Čemu je rovna hodnota  ?
?
c) Speciálně si nakonec napište vztah 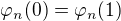 .
.
Offline
- (téma jako vyřešené označil(a) Marian)
#2 07. 02. 2017 16:30
#3 08. 02. 2017 04:39
Re: Funkce s parametrem
↑ check_drummer:
Vycházím ze své střední školy, takže derivování připouštím. Mohl jsem to připomenout v zadání úlohy.
Offline
#4 20. 02. 2017 20:22
Re: Funkce s parametrem
Vzhledem k tomu, že žádné nápady nejsou doposud prezentovány, uvedu své řešení využívající derivace funkce
Derivujme danou funkci podle proměnné z:![kopírovat do textarea $
\varphi'_n(z)
&=\sum_{j=1}^{n}\left (z^{j-1}-{n\choose j}\cdot (z-1)^{j-1}\right )\\[2mm]
&=\sum_{j=1}^{n}z^{j-1}-\frac{1}{z-1}\cdot\sum_{j=1}^{n}{n\choose j}\cdot (z-1)^j.
$](/mathtex/d8/d883ad2798ba59e50691a28640c5ceae.gif)
Dále sečteme první součet jako součet prvních n členů geometrické posloupnosti a druhý součet lze psát v uzavřeném tvaru užitím binomické věty. Dostáváme
Derivace je nulová, tedy  je konstantní.
je konstantní.
Dosadíme-li 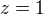 , je zřejmé, že
, je zřejmé, že  je rovno n-tému harmonickému číslu. Dosadíme-li
je rovno n-tému harmonickému číslu. Dosadíme-li 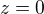 , dostáváme z konstantnosti studované funkce a z předchozího dosazení jiné vyjádření harmonického čísla:
, dostáváme z konstantnosti studované funkce a z předchozího dosazení jiné vyjádření harmonického čísla:
Dosazením jiných hodnot lze najít další vyjádření harmonického čísla (např. pro z=1/2 apod.).
Závěrem poznamenávám, že harmonická čísla hrají významnou roli při určité formulaci slavné Riemannovy hypotézy, viz část Applications v odkazu výše.
Offline
#5 21. 02. 2017 13:43
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Funkce s parametrem
↑ Marian:
Ahoj, to je i mé řešení, ale nechtěl jsem středoškolákům kazit radost. :-)
"Máte úhel beta." "No to nemám."
Offline
#6 21. 02. 2017 17:53
Re: Funkce s parametrem
↑ check_drummer:
Původní příspěvek jsem editoval a omezil proměnnou  na reálnou. Pro středoškoláky totiž není standardní derivovat funkci komplexní proměnné.
na reálnou. Pro středoškoláky totiž není standardní derivovat funkci komplexní proměnné.
Existuje však elementární postup, který nepoužívá pojem derivace (představil mi jej uživatel Pavel z tohoto fóra). Snad najde čas, aby svůj zajímavý příspěvek uveřejnil.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » Funkce s parametrem (TOTO TÉMA JE VYŘEŠENÉ)


 :
:![kopírovat do textarea $
\varphi_n(z)
&=\sum_{j=1}^{n}\left (\frac 1j(z-1+1)^j-\frac 1j{n\choose j}(z-1)^j\right )
=\sum_{j=1}^{n}\sum_{k=0}^{j}\frac 1j{j\choose k}(z-1)^k-\sum_{j=1}^{n}\frac 1j{n\choose j}(z-1)^j\\[\baselineskip]
\varphi_n(z)
&=\sum_{j=1}^{n}\sum_{k=0}^{j}\frac 1j{j\choose k}(z-1)^k-\sum_{j=1}^{n}\frac 1j{n\choose j}(z-1)^j\\[.5\baselineskip]
&=\sum_{j=1}^{n-1}\sum_{k=0}^{j}\frac 1j{j\choose k}(z-1)^k+\sum_{k=0}^{n}\frac 1n{n\choose k}(z-1)^k-\sum_{j=1}^{n}\frac 1j{n\choose j}(z-1)^j\\[.5\baselineskip]
&=\sum_{j=1}^{n-1}\sum_{k=0}^{j}\frac 1j{j\choose k}(z-1)^k+\frac 1n+\sum_{j=1}^{n}\left(\frac 1j{n-1\choose j-1}(z-1)^j-\frac 1j{n\choose j}(z-1)^j\right)\\[.5\baselineskip]
&=\frac 1n+\sum_{j=1}^{n-1}\sum_{k=0}^{j}\frac 1j{j\choose k}(z-1)^k-\sum_{j=1}^{n}\frac 1j{n-1\choose j}(z-1)^j\\[.5\baselineskip]
&=\frac 1n+\sum_{j=1}^{n-1}\sum_{k=0}^{j}\frac 1j{j\choose k}(z-1)^k-\sum_{j=1}^{n-1}\frac 1j{n-1\choose j}(z-1)^j\\[.5\baselineskip]
&=\frac 1n+\varphi_{n-1}(z)
$](/mathtex/37/379bd87f561c48db3b2ed5e4a5e3b11b.gif)
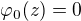 , můžeme psát
, můžeme psát