Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 07. 02. 2017 22:13 — Editoval Pritt (07. 02. 2017 22:15)
#3 13. 02. 2017 10:44 — Editoval Rumburak (13. 02. 2017 12:22)
Re: Důkaz metrického prostoru
↑ holyduke:
Ahoj.
Technicky jednodušší bude nejprve ukázat, že předpisem
![kopírovat do textarea $|| f || := \max_{x \in [a, b]} |f(x)|$](/mathtex/ff/ff6bc637baed753b398220ec1937a9e7.gif)
je definována norma na prostoru  , tj. že pro libovolná
, tj. že pro libovolná 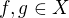 a libovolné reálné
a libovolné reálné  platí
platí
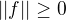 ,
,
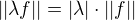 ,
,
![kopírovat do textarea $||f|| = 0 \Rightarrow f(x) = 0 \text{pro každé} x \in [a, b]$](/mathtex/44/449196e6b71e031cd05c7223384d7ed4.gif) ,
,
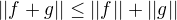 .
.
Důkaz, že 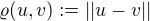 je metrika na prostoru
je metrika na prostoru  , je pak jasný.
, je pak jasný.
Offline


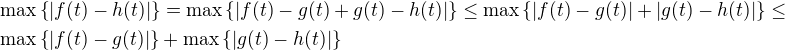 .
.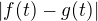 a
a 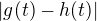 budou mít maximum ve stejném bodě.
budou mít maximum ve stejném bodě.