Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 20. 04. 2017 18:03
Re: Samá ostrá maxima
Podla mna je to tak, ze v R nemoze.
Offline
#3 20. 04. 2017 18:34
Re: Samá ostrá maxima
Offline

 . Pre kazde
. Pre kazde  existuju jednoznacne dane cele nesudelitelne cisla
existuju jednoznacne dane cele nesudelitelne cisla 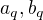 take, ze
take, ze  a
a 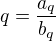 . Da sa overit, ze funkcia
. Da sa overit, ze funkcia  nadobuda v kazdom bode ostre lokalne maximum.
nadobuda v kazdom bode ostre lokalne maximum. . Ak by sme chceli zacovat to, ze v racionalnych cislach ostanu lokalne maxima, tak pre iracionalne
. Ak by sme chceli zacovat to, ze v racionalnych cislach ostanu lokalne maxima, tak pre iracionalne  by muselo platit
by muselo platit 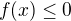 , avsak potom toto by nemohlo byt bodom lokalneho maxima. V tomto priklade vidime, ze "problem"
, avsak potom toto by nemohlo byt bodom lokalneho maxima. V tomto priklade vidime, ze "problem"  nadobuda ostre lokalne maximum v kazdom bode.
nadobuda ostre lokalne maximum v kazdom bode. , potom
, potom  .
.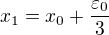 , potom
, potom  .
. , potom
, potom  .
. a teda
a teda  .
. je Cauchyovska a musi konvergovat k nejakemu
je Cauchyovska a musi konvergovat k nejakemu 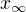 a kedze je aj rastuca, tak
a kedze je aj rastuca, tak  a z 3) dostavame, ze
a z 3) dostavame, ze  . Avsak v kazdom okoli
. Avsak v kazdom okoli