Matematické Fórum

Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.

Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.

Nejste přihlášen(a). Přihlásit

Stránky: 1

 

#1 29. 05. 2017 12:21

Verčák
Zelenáč
Příspěvky: 4
Škola: ČVUT FJFI
Pozice: Student
Reputace:   1 
 

Maclaurinův polynom

Ahoj, prosila bych o pomoc s výpočtem Maclaurinova polynomu druhého stupně funkce:

$g(x) = \sqrt{1-\mathrm{e}^{3x}}$

Obecně vím, že Maclaurinův polynom je Taylorův polynom v bodě 0 a to mi právě dělá u tohoto příkladu problém. Do vzorce pro Maclaurinův polynom přece dosazuji hodnotu derivací v bodě 0. První derivaci mám: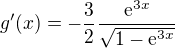

$g'(x) = -\frac{3}{2}\frac{\mathrm{e}^{3x}}{\sqrt{1-\mathrm{e}^{3x}}}$

která v 0 není definovaná, resp tam dělím nulou.

Je tento příklad vůbec řešitelný? Pokud ne, jak to obhájit?

Děkuji moc za jakékoli rady.

Offline

  • (téma jako vyřešené označil(a) Verčák)

#2 29. 05. 2017 13:26

Eratosthenes
Příspěvky: 2764
Reputace:   136 
 

Re: Maclaurinův polynom

ahoj ↑ Verčák:

derivace v nule skutečně neexistuje, takže neexistuje ani požadovaný rozvoj.

Budoucnost patří aluminiu.

Offline

 

 

Stránky: 1

Zápatí

Powered by PunBB
© Copyright 2002–2005 Rickard Andersson