Matematické Fórum

znamená to, že relativistická hmotnosť neovplyvňuje gravitačné sily? napr. preletí ked asteorid okolo planéty rôznou rýchlosťou tak gravitačné sily ktoré budú pôsobiť v bode kde je najbližšie k ťažisku tak budú záležať iba kľudovej hmotnosti asteroidu.

Je to trochu složitější a zkusím odpovědět tak nějak z historického konceptu, protože to mělo dost vliv na to, proč se vlastně některé veličiny zavedly do dnešní podoby.

Hmotnost se vyskytuje v mnoha fyzikálních zákonech.

* Lze díky ní (se znalostí hmotnosti elementárnách částic) stanovit kolik dané látky je
* Je v gravitačním zákoně
* Je v Newtonově zákonu síly
* Je v hybnosti o které víme, že se zachovává.

a asi bychom vymysleli ještě nějaké další. Kromě toho prvního se zjistilo (po příchodu Alberta Einsteina a jeho TR), že jenom hmotnost nestačí. Protože ale modifikované vztahy měly často ten tvar, že místo hmotnosti se objevilo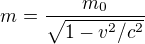

,

tak se celá ta levá strana začínala nazývat relativistickou hmotností, ačkoli hmotnost jako taková (která vyjadřuje množství materiálu) by měla zůstat ona klidová hmotnost . Relativistická hmotnost si též našla zastoupení v nově odvozeném vztahu



Naschvál jsem jej rozvinul i do vyjádření v klidové hmotnosti, protože to o dost lépe vysvětluje, o co tam jde. V čitateli máme konstanty a energie závisí díky tomuto vztahu skutečně na rychlosti, což není nic překvapivého. Jiný vzoreček pro kinetickou energii tvrdí totéž, jen ne tolik přesně.

Zavedení pojmu relativistická hmotnost tak souvisí hlavně s tím, že je to užitečná substituce v mnoha vztazích, po příchodu teorie relativity (spíše však té speciální).

V gravitačním zákoně, ale hmotnost vystupuje složitěji, proto nám náhrada za relativistickou hmotnost nestačí. Kdybychom vzali dvě hmotné tělesa a vyslali je pohybovat kolmo k jejich spojnici, tak jejich vzájemné gravitační urychlení směrem k sobě se nám bude jevit dokonce nižší, ačkoli relativistická hmotnost vzroste.

(Nebrat úplně vážně: Analogie je s pohybem elektrických nábojů. Náboje stejného znaménka se odpuzují, ale při paralelním pohybu se toto odpuzování snižuje a proto se pak vodiče vedoucí proud stejným směrem přitahují. Jedná se o alternativní relativistické vysvětlení účinků magnetického pole.)

Do gravitačního zákona tedy není dobré míchat relativistickou hmotnost. Pro pomalé pohyby hmotných těles lze získat přesnější vztahy díky tzv. gravitoelektromagnetismu

https://en.wikipedia.org/wiki/Gravitoelectromagnetism

Sepsal jej Oliver Heaviside těsně před Einsteinem. Popisuje rovnice gravitace úplně analogicky jako je popis elektromagnatických sil pomocí elektrického a magnetického pole.

Poměrně záhy na to však Albert Einstein přišel s obecnou teorií relativity, takže gravitoelektromagnetismus se nikdy reálně moc nevyužil. Ale třeba na vyřešení úlohy dvou rychle letících hmotných částic a řešení gravitační přitažlivosti mezi nimi je gravitoelektromagnetismus docela dobrý. Jen tenhle příklad není úplně typický. U rychle letících částic obvykle neřešíme gravitaci.

Jakmile se dopátráváme k extrémům, jako jsou černé díry, již ani gravitoelektromagnetismus zcela nestačí je třeba použít čistě OTR. Tam v gravitačním zákoně potřebujeme znát tenzor energie a hybnosti a gravitace zcela postrádá význam síly. Vše se nám zde pohybuje rovnoměrně přímočaře, ale na zakřiveném pozadí, takže pak pozorujeme ohnuté trajektorie.