Matematické Fórum

Nikd0 · 31. 08. 2017 18:53

Zdravím,

řeším numerickou úlohu - mám obyčejnou diferenciální rovnici druhého řádu, zadanou funkční hodnotu v bodě $a$ a derivaci v bodě $b$ . Řeším metodou střelby - vycházím pod různými derivacemi z bodu $a$ a zkouším, s jakou derivací dojdu do $b$ .

Zadání je $y''=f_1(x)y'+f_2(x)y+f_3(x), y(a)=c, y'(b)=d$ , kde $f_i$ jsou libovolné spojité funkce. S řešením problém nemám, ale nejsem si jistý, proč to funguje a zda to funguje vždy.
Správnost mého řešení závisí na tom, že s rostoucí volenou derivací v $a$ roste i ta v $b$ . Zkoušel jsem dosadit několik rovnic, a vždy to platilo. Všiml jsem si také, že závislost $y'(a)\mapsto y'(b)$ vypadá jako lineární (a nutně prochází nulou). Můžete mi to potvrdit? Napadlo mě, že to je zaručeno právě druhým řádem diferenciální rovnice, ale nijak jsem to nedokázal.

kaja.marik · 03. 10. 2017 14:11

Mam protipriklad. Treba 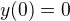$y''=-y$ , $y(0)=0$ . Resenim je $y=K\sin(x)$ a pokud roste $y'(0)$ tak $y'(\pi)$ klesa.

Brano · 03. 10. 2017 16:42 — Editoval Brano (03. 10. 2017 16:46)

↑ Nikd0:
rastucost tam ani nepotrebujes; ty len potrebujes aby priradenie $y'(a)\mapsto y'(b)$ bolo dostatocne slusne. Spojitost myslim zarucia nejake zakladne vety o ODR a potom mozes riesenie hladat trebars metodou regula falsi - ta aby skonvergovala potrebuje nejake predpoklady, ale na druhu stranu principialne nic overovat nemusis. Ak skonverguje, tak je to riesenie a ak nie tak skusis nieco ine.

ak vsak chces so zaujmu overit kedy presne funguje tvoja metoda, tak ju napis a mozeme porozmyslat; ako uz bolo povedane; rastucost zarucenu nemas.

Matematické Fórum

#1 31. 08. 2017 18:53

Závislost derivace v bodě b na derivaci v a (metoda střelby)

#2 03. 10. 2017 14:11

Re: Závislost derivace v bodě b na derivaci v a (metoda střelby)

#3 03. 10. 2017 16:42 — Editoval Brano (03. 10. 2017 16:46)

Re: Závislost derivace v bodě b na derivaci v a (metoda střelby)

Zápatí