Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 01. 10. 2017 11:08
Množiny
Dobrý den,
Mám 2 příklady, které mi připadají na stejným principu a to je ten problém, protože ve skutečnosti je výsledek jiný.
Příklad 1:
A = (-5; 10>
B = <0; 4>
B/A =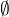 
Příklad 2:
A = N
B = <1; 2>
Myšlenka: B/A =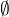
Skutečnost: B/A = (1; 2)
Řešil jsem to i podle grafu, abych to lépe viděl. Jenže A = N mi trochu redukuje jistotu. Myslím, že by to mělo být <0; +
), protože když je uzavřený interval u nuly, tak ji nepočítáme. S touto úvahou graf vypadá ve srovnání s grafem prvního příkladu tak, že výsledek by měl být stejný.
Prosím o pomoc.
Offline
#2 01. 10. 2017 11:17 — Editoval Akraell (01. 10. 2017 11:21)
Re: Množiny
Ještě se vlastně A = N z logického hlediska dá zapsat (1; +). Tím by se počítala i jednička a graf by vypadal trochu jinak. Ale stejně nerozumím, proč je výsledkem (1; 2)
no ne, teprve teď mi došlo, že zápis je spíš {1;2;3;4;5;.....}. Ale ještě řeším důvod výsledku
Offline
.
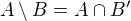