Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 10. 2017 11:27
Rychlost
Ahoj, chci se zeptat, jaktoze plati tento vztah pro rychlost? Rozumim tomu, ze rychlost se rovna derivaci polohoveho vektoru podle casu, ale neni mi jasne, jak zderivovali tu slozenou funkci, kde polohovy vektor je funkci drahy a draha je funkci casu, mohl by mi prosim nekdo napsat matematicky postup? Dale nevim, proc plati, ze derivace polohoveho vektoru podle drahy je rovna tecnemu vektoru? Dekuji za odpoved.
Offline
#2 11. 10. 2017 13:04 — Editoval mracek (11. 10. 2017 13:09)
Re: Rychlost
Tecna v bode [x0,y0] se pocita jako prvni derivace funkce.
http://www.aristoteles.cz/matematika/fu … iklady.php
A ten zbytek snad poradi nekdo jiny asi lepe.
Slozena derivace se derivuje na 2x
y = funkce(x)
y' = dy / dx = d(funkce(x)) / dx
y = funkce(x) ... s = funkce(v,t) = v * t
y = funkce(u) ... s = funkce(a,t) = a * t * t
u = funkce(x) ... a = funkce(v,t) = v / t
y' = dy / dx
= dy / du * du / dx
= d(y=funkce(u)) / du * d(u=funkce(x)) / dx
= ds / dv = d(v * t) / dv = t ... [1]
= ds / da * da / dv
= d(a * t * t)/da * d(v / t)/dv
= t * t * 1/t
= t ... [2]
Derivace rychlosti podle v vysla t. Derivace jinou funkci, jejich nasobenim dostanes rychlost, derivovana kazda zvlast dostavas stejny vysledek.
d(v / t)/dv = 1/t * d(v)/dv = 1/t
d(x / 5)/dx = 1/5 * d(x)/dx = 1/5
d(x * x / 5)/dx = 1/5 * d(x * x)/dx = 1/5 * 2 * x ... normani derivovani, co neni x, je konstanta, at uz je tam napsane T nebo cislo 5.
https://cs.wikipedia.org/wiki/Z%C3%A1pis_derivace
Offline
#3 11. 10. 2017 17:33
Re: Rychlost
↑ linet123:
tady se předpokládá, že máš vyjádřené 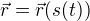 a pak prostě derivuješ složenou funkci.
a pak prostě derivuješ složenou funkci.
To možná záš jinak zapsané![kopírovat do textarea $[(f(g(x))]^\prime=f^\prime(g(x))\cdot g^\prime(x)$](/mathtex/75/75a095ecb061c05cc93dedef63d37471.gif)
ale to je jen jiný zápis![kopírovat do textarea $[(f(g(x))]^\prime=\frac{\mathrm{d} f}{\mathrm{d} g}\cdot\frac{\mathrm{d} g}{\mathrm{d} x}$](/mathtex/09/09e6afbcc2d918cce1ad76fb083d2b4a.gif)
Takže žádný jiný matematický postup nedostaneš, protože to je jen jiný způsob zápisu.
Ke druhé otázce:
Musíš vědět, jak je definovaná funkce 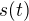 . A to je
. A to je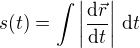 - DEFINICE
- DEFINICE
z toho ale přímo plyne, že 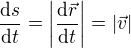
dále musíš vědět, že každý vektor můžeš zapsat 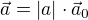 , kde
, kde 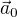 je jednotkový vektor ve směru vektoru
je jednotkový vektor ve směru vektoru  .
.
Takže tvůj vztah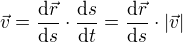
a současně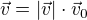
z čehož jasně plyne 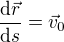
Takže 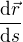 je jednotkový vektor ve směru rychlosti, a tím pádem je tečný vektor k trajektorii v daném bodě, protože rychlost je derivace a geometrický význam derivace je směrnice tečny v příslušném bodě.
je jednotkový vektor ve směru rychlosti, a tím pádem je tečný vektor k trajektorii v daném bodě, protože rychlost je derivace a geometrický význam derivace je směrnice tečny v příslušném bodě.
Snad to takto stačí.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#4 11. 10. 2017 17:56
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Rychlost
y = funkce(x) ... s = funkce(v,t) = v * t
y = funkce(u) ... s = funkce(a,t) = a * t * t
u = funkce(x) ... a = funkce(v,t) = v / t
y' = dy / dx
= dy / du * du / dx
= d(y=funkce(u)) / du * d(u=funkce(x)) / dx
= ds / dv = d(v * t) / dv = t ... [1]
= ds / da * da / dv
= d(a * t * t)/da * d(v / t)/dv
= t * t * 1/t
= t ... [2]
Derivace rychlosti podle v vysla t. Derivace jinou funkci, jejich nasobenim dostanes rychlost, derivovana kazda zvlast dostavas stejny vysledek.
d(v / t)/dv = 1/t * d(v)/dv = 1/t
d(x / 5)/dx = 1/5 * d(x)/dx = 1/5
d(x * x / 5)/dx = 1/5 * d(x * x)/dx = 1/5 * 2 * x ... normani derivovani, co neni x, je konstanta, at uz je tam napsane T nebo cislo 5.
Tohle není správně, s výjimkou těchto tří řádků:
y' = dy / dx
= dy / du * du / dx
= d(y=funkce(u)) / du * d(u=funkce(x)) / dx
Důvod je, že nemůžeš vytýkat proměnnou z diferenciálu: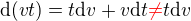
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#5 12. 10. 2017 08:26
Re: Rychlost
↑ KennyMcCormick:
Jo, to sem presne cekal, ze se nekdo ozve :)
Mas funkci y = func(x)
Kdyz to derivujes 'podle x', tak, cokoliv, co neni x muzes vytknout pred diferencial, pokud to jde vytknout.
d(v*t)/dt = v * d(t)/dt
d(v*t)/dv = t * d(v)/dv
To, co pises ty, jako nerovnost, jsem vubec nenapsal, vis.
Offline
#7 12. 10. 2017 21:31
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Rychlost
To, co pises ty, jako nerovnost, jsem vubec nenapsal, vis.
Používáš ji tady:
↑ mracek:
ds / dv = d(v * t) / dv = t
a tady:
d(a * t * t)/da * d(v / t)/dv
= t * t * 1/t
Jestli chceš, vyber si jeden z těch dvou případů, vysvětlím ti to na něm.
Kdyz to derivujes 'podle x', tak, cokoliv, co neni x muzes vytknout pred diferencial, pokud to jde vytknout.
d(v*t)/dt = v * d(t)/dt
d(v*t)/dv = t * d(v)/dv
To je ta samá chyba zopakovaná podruhé.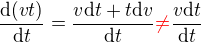
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline


