Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » V zadaném intervalu nalezněte všechny lokální extrémy
#1 16. 10. 2017 19:53
V zadaném intervalu nalezněte všechny lokální extrémy
Dobrý den,
Mám napsat program, který v zadaném intervalu < > nalezne všechny lokální extrémy (minima nebo maxima) kubické funkce f(x) = ax^3 + bx^2 + cx + d
> nalezne všechny lokální extrémy (minima nebo maxima) kubické funkce f(x) = ax^3 + bx^2 + cx + d
Tip: Funkci procházejte v cyklu s krokem delta = 0.001. Pro extrém platí, že dvě po sobě jdoucí diference (f(x - delta) - f(x) a f(x) - f(x + delta)) mají opačná znaménka.
Výsledkem programu má být načtení z klávesnice hodnoty a, b, c, d, x1, x2 a program má podle toho najít lokální extrémy.
Problém je, že nevím, jaká jsou matematická pravidla. Ani nevím, k čemu tam slouží delta.
Offline
#2 17. 10. 2017 11:29 — Editoval Rumburak (19. 10. 2017 11:00)
Re: V zadaném intervalu nalezněte všechny lokální extrémy
Ahoj.
Z praktických důvodů změním označení 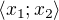 na
na  , kde
, kde  .
.
Doporučený tip je v zásadě správný, ale řídit se jím doslova by mohlo vést ke komplikacím,
proto ho poněkud modifikujme.
I. Najděme přirozené číslo  takové, aby
takové, aby  , a položme
, a položme
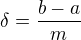 .
.
II. Definujme konečnou posloupnost  předpisem
předpisem
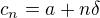 .
.
Zřejmě  .
.
III. V cyklu pro  hledejme taková
hledejme taková  , pro něž je splněna podmínka
, pro něž je splněna podmínka
 .
.
Nalezaná čísla 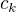 jsou aproximacemi bodů uvnitř stanoveného intervalu, v nichž nastávají
jsou aproximacemi bodů uvnitř stanoveného intervalu, v nichž nastávají
lokální extrémy.
Jak posoudit situaci v jeho krajních bodech, je snad jasné.
EDIT. Oprava překlepu a chyb v kroku III.
Offline
#3 17. 10. 2017 11:33 — Editoval Rumburak (17. 10. 2017 11:33) Příspěvek uživatele Rumburak byl skryt uživatelem Rumburak.
#4 17. 10. 2017 15:32
Re: V zadaném intervalu nalezněte všechny lokální extrémy
Děkuji za první zpětnou vazbu.
Je tu ale stále problém.
Např. když zadám hodnoty, že to bude mít toto zadání: ,
, 
Tak výsledek musí být: 
Nevím jestli jsem počítal správně (ani jsem ještě nepochopil jak mám hledat  a k, takže jsem třetí část zatím nepočítal), ale když:
a k, takže jsem třetí část zatím nepočítal), ale když:
nechám "delta = 0,001"
za  dosadím -4
dosadím -4
za  dosadím -2 (vyšlo mi, že pro -2 je m = 2000. Snad jsem počítal a pochopil správně..)
dosadím -2 (vyšlo mi, že pro -2 je m = 2000. Snad jsem počítal a pochopil správně..)
Tak ta výsledná hodnota maximum = -3.33 bude pro  a jestli má být n-tý člen přirozený číslo, tak jsem prohrál.
a jestli má být n-tý člen přirozený číslo, tak jsem prohrál.
Offline
#5 17. 10. 2017 16:46 — Editoval Rumburak (17. 10. 2017 16:56)
Re: V zadaném intervalu nalezněte všechny lokální extrémy
↑ Akraell:
A jak jsi došel k "výsledné hodnotě" -3.33 pro maximum ?
Bod, v němž skutečně nastane extrém, nemusí být členem posloupnosti 
a že to tak bude, je i málo pravděpodobné.
Řešení, k nimž vedou numerické metody, jsou obecně jen méně či více přibližná.
V tom možná spočívá problém, na který upozorňuješ.
Offline
#6 17. 10. 2017 17:26
Re: V zadaném intervalu nalezněte všechny lokální extrémy
K tomu zadání mi napsali 4 příklady, jak má vypadat výstup. Uvedu 2 z nich:
Příklad spuštění programu 1:
Zadej koeficient a:
0.1
Zadej koeficient b:
-1
Zadej koeficient c:
-10
Zadej koeficient d:
50
Zadej pocatek intervalu:
-6
Zadej konec intervalu:
-4
=> Protože v daném intervalu neleží žádný extrém, program nic nevypíše
Příklad spuštění programu 2:
Zadej koeficient a:
0.1
Zadej koeficient b:
-1
Zadej koeficient c:
-10
Zadej koeficient d:
50
Zadej pocatek intervalu:
-4
Zadej konec intervalu:
-2
max: -3.33
To je asi ten důvod, proč mám doporučeno "Delta = 0,001", protože když si vymyslím jiný m, tak pak to vychází jinak.
Offline
#7 18. 10. 2017 05:21
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: V zadaném intervalu nalezněte všechny lokální extrémy
V čem přesně je teď problém? :)
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#8 18. 10. 2017 09:35
Re: V zadaném intervalu nalezněte všechny lokální extrémy
↑ KennyMcCormick:
Nevím jaký vzorečky do programu vložit, aby výstup programu odpovídal zadání a měl shodu s očekávaným výstupem.
Zatím mě napadá jen vytvořit posloupnost, která bude dosazovat za x čísla v intervalu od a; a + 0,01; a + 0,02... do b. Pak vyhledá maximum a minimum s podmínkou, že monotonie např. rostoucí se začala měnit na klesající.
Jenže to je docela blbost, protože někdo vyplní obrovský interval a může si třeba mezitím jít hrát šachy než vyleze výsledek.
Offline
#9 18. 10. 2017 10:16
Re: V zadaném intervalu nalezněte všechny lokální extrémy
↑ Akraell:
Pokud to dobře chápu, tak tebou právě navržený postup je naprosto přesně to samé, co doporučují v zadání a co ti rozepsal Rumburak - jen s tím rozdílem, že doteď jste se bavili o kroku 0.001, nikoli 0.01. A pokud to budeš programovat na počítači mladším než nějakých 60 let, tak mezitím nestihneš ani rozestavit figurky na šachovnici, a to i v případě dost velkého intervalu. Samozřejmě pro EXTRÉMNĚ velké intervaly to vhodné není, ale v takovém případě se dají použít zase jiné metody. V tomto případě to například jde derivováním převést na rovnici typu polynom(x)=0, která se dá řešit různými (a mnohem efektivnějšími) způsoby.
Z toho co píšeš jsi to zatím nenaprogramoval. Takže doporučuji už o tom moc nešpekulovat, udělat to a pak zkoumat výsledky. Že netrefiš přesně hodnotu -3.33, jak "chtějí", je celkem jedno (on tam ten extrém ani přesně není). Ale tvá chyba bude maximálně 0.001, takže....
Offline
#10 18. 10. 2017 19:48
Re: V zadaném intervalu nalezněte všechny lokální extrémy
Aha, já v tom celou dobu hledal nějakou složitost včetně toho, co psal Rumburak.
Jeden žák to řešil pomocí integrací, že mu odpadlo cyklení programu. Já ještě zatím nevím, co jsou derivace a integrace. Je toho dost a budu to muset dohnat. Takže mě tu asi ještě "párkrát" uvidíte a asi to bude s mojí hlavou opět na dlouho (a to jsem dal maturitu z matematiky na 80%) :D
Děkuji moc za vaší pevnou spolupráci
Vážím si toho.
Offline
#11 19. 10. 2017 11:03
Re: V zadaném intervalu nalezněte všechny lokální extrémy
↑ Akraell:
Ahoj.
V kroku III. mého příspěvku ↑ Rumburak: byla ještě jedna chyba,
dokonce zásadního významu. Již opraveno.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » V zadaném intervalu nalezněte všechny lokální extrémy
