Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 18. 10. 2017 23:36
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Konstrukce 4úhelníku
A čo si zatiaľ skúsila resp. kde si sa zasekla?
Ja by som to videl na dve polpriamky pod tými zadanými uhlami, a potom na prieniky vhodných rovnobežiek a kružníc...
Offline
#3 19. 10. 2017 07:47 Příspěvek uživatele mracek byl skryt uživatelem jelena. Důvod: viz samostatné téma
#4 19. 10. 2017 07:59 Příspěvek uživatele mracek byl skryt uživatelem Stýv.
#5 19. 10. 2017 08:05 Příspěvek uživatele Al1 byl skryt uživatelem jelena. Důvod: viz samostatné téma
#6 19. 10. 2017 10:50
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Konstrukce 4úhelníku
Zdravím,
spíš než technikou sestrojení, bych začínála rozborem a z toho mi plyne, že přímou konstrukci čtyřúhelník nesestrojím, musím využit pomocnou konstrukci, která může být založena na posunutí (tedy rovnoběžky jako takové určitý smysl mají) a sestrojení pomocného trojúhelníku sus, kde úhel odvodím ze zadaných.
↑ aniuce: co Tobě plynulo z rozboru? Děkuji.
Offline
#7 20. 10. 2017 18:59
Re: Konstrukce 4úhelníku
Pozdravujem ↑ jelena:,
Presne ako pises, aj ja to vidim tak ako pises : treba pouzit metodu : Analyza- Synteza.
A tak rozbor umozni urcit prvky ktore, ktore ukazu ako realizovat (eukdlidosku) konstrukciu. A tiez ju podrobne umozni popisat, co je synteza problemu. A pochopitelne kazdy takyto problem sa ukoncuje diskuziou riesitelnosti vo vsetkych moznych situaciach.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 21. 10. 2017 11:15 Příspěvek uživatele vlado_bb byl skryt uživatelem jelena. Důvod: viz samostatné téma
#11 21. 10. 2017 12:23
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Konstrukce 4úhelníku
Zdravím,
↑ aniuce: pokud máš dokonce zadané konkrétní hodnoty úhlů, situace je usnadněna. Ve všeobecném případě bys musela ještě provést "rozřadění" různých případů velikostí úhlu (např. pokud oba budou tupé) a uspořádat velikosti. Ale princip sestrojení zůstává stejný.
Pokud jsi dělala rozbor, tak u strany  (s nezadanou délkou) jsou úhly
(s nezadanou délkou) jsou úhly  a
a  , přičemž délky stran DC a AB máš. Zde můžeš využit posunutí jedné ze stran AB nebo DC ve směru strany d tak, aby vznikl pomocný trojúhelník. Stranu
, přičemž délky stran DC a AB máš. Zde můžeš využit posunutí jedné ze stran AB nebo DC ve směru strany d tak, aby vznikl pomocný trojúhelník. Stranu  jen naznačíš, abys udala směr a zvolíš na ni jeden z bodu D nebo A. Stačí tak pro další krok? Děkuji.
jen naznačíš, abys udala směr a zvolíš na ni jeden z bodu D nebo A. Stačí tak pro další krok? Děkuji.
↑ vanok: ano - zakreslení toho, co je zadáno, + rozbor nemá být vynechán. Jinak lze dlouho setrvat u kreslení rovnoběžek. U nás teď bylo vystoupení (bohužel, malá návštěvnost) a pokud se vybavím, tak v novele zrovna povídá něco ve smyslu "pokud se chceš někam dostat, představ si, že jsi již tam". V konstrukčních úlohách také tak. Také pozdravy.
Offline
#12 21. 10. 2017 12:38
Re: Konstrukce 4úhelníku
Analyza -rozbor
( mozes vyuzit na nacrty a potom aj na konstrukciu GeoGebru)
Predpokladaj, ze tvoj stvoruholnik sa da konstruhovat a je to stvoruholnik ABCD taky, ze AB=a,BC=b,CD=c a tiez uhol v A je  a uhol v D je
a uhol v D je  .
.
Predpokladaj, ze DA=d.
Je jednoduche konstatovat, ze ak nahradime  z
z 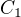 a
a  z
z 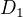 tak ze
tak ze  a
a  a
a 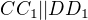 , ze
, ze  ma strany a uhly . ... a potom ako sa da z neho vratit k
ma strany a uhly . ... a potom ako sa da z neho vratit k 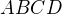 ????
????
Pokracuj.
( vsetko kresli !)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#14 21. 10. 2017 14:50 — Editoval vanok (21. 10. 2017 18:08)
Re: Konstrukce 4úhelníku
Ahoj,
Podla analyzy co som ti navrhol, ta etapa od  k
k 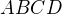 ,
,
sa urobi vdaka konstrukcii bodov 
Konsrtrukcia bodu  :
:
priesecik priamky  cez bod
cez bod 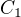 rovnobeznu z
rovnobeznu z 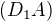 a kruznici centra
a kruznici centra 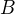 a polomeru
a polomeru  , da bod
, da bod  .
.
Konstrukcia bodu  : tu necham na teba.
: tu necham na teba.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#15 22. 10. 2017 15:07 Příspěvek uživatele mracek byl skryt uživatelem jelena. Důvod: viz samostatné téma
#16 22. 10. 2017 16:44 Příspěvek uživatele jelena byl skryt uživatelem jelena. Důvod: viz samostatné téma
#17 23. 10. 2017 13:17 — Editoval mracek (23. 10. 2017 13:18)
Re: Konstrukce 4úhelníku
↑ jelena: Tema jsem rano vytvoril, ale uz neexistuje.
http://forum.matweb.cz/viewtopic.php?pid=552813
(Hlavni stranka > Ostatni)
Offline
#20 24. 10. 2017 14:30 — Editoval Ferdish (24. 10. 2017 14:31)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Konstrukce 4úhelníku
↑ aniuce:
Neviem, či je možné naviesť ťa k správnemu riešeniu ešte viac, než urobil kolega Vanok. Už snáď len podrobný, kompletný postup konštrukcie...nakoľko jeho návrh riešenia neobsahuje žiadnu chybu, ktorá by mi dovoľovala do toho zasahovať, nechávam to na ňom.
Offline
#21 24. 10. 2017 15:10 — Editoval vanok (25. 10. 2017 11:56)
Re: Konstrukce 4úhelníku
↑ aniuce:,
Ked si sledovala analyzu- rozbor, tak je ti iste jasne, ze konstrukciu ABC1D1 mozes urobit takto.
1) narysuj D1A (podla rozboru to moze byt lubovolna nenulova usecka
2) narysuj body C1 a B ( uhly su ...  a dlzka
a dlzka 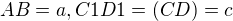
Zvysok iste dokoncis
Edit: oprava preklepu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#22 25. 10. 2017 11:43 — Editoval jelena (25. 10. 2017 11:57)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Konstrukce 4úhelníku
↑ vanok:
Zdravím,
ještě jsem procházela téma, zda máme odlišné metody, ale ne. Oba uvažujeme posunutí ve směru přímky 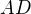 (
( ), není to směr orientovaný, jelikož můžeme zvolit posunutí jak bodu
), není to směr orientovaný, jelikož můžeme zvolit posunutí jak bodu  (a návazně úsečky
(a návazně úsečky  ), tak i bodu
), tak i bodu  (a návazně úsečky
(a návazně úsečky 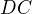 ). "Mé" posunutí posouvá bod
). "Mé" posunutí posouvá bod  přímo do bodu
přímo do bodu  , čímž vzníká pomocný trojúhelník
, čímž vzníká pomocný trojúhelník  (úhel
(úhel  se buď dopočte ze zadaných
se buď dopočte ze zadaných  ,
,  , nebo rovnou vznikne sestrojením úhlů
, nebo rovnou vznikne sestrojením úhlů 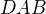 a
a 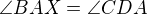 všechno ve vrchlu
všechno ve vrchlu  , do kterého jsem posunula bod
, do kterého jsem posunula bod  ).
).
Tvé posunutí posouvá bod  do libovolného bodu na přímce
do libovolného bodu na přímce 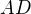 .
.
Akorát jsem neporozuměla návodu v ↑ příspěvku 21:, konkrétně bod 2) označení úhlů. Děkuji za upřesnění.
edit: opraveno, že v příspěvku 21
Offline
#23 25. 10. 2017 12:21
Re: Konstrukce 4úhelníku
Pozdravujem ↑ jelena:,
Co sa tyka uhlov, to bol preklep je to opravene, dakujem za upozornenie.
Je jasne, ze obe riesenia su zaujimave, to moje som naviazal na analyzu ktoru som vyssie urobil.
Bolo by zaujimave sprevadzat nacrtmy, ( geogebra moze posluzit, no na mobile to nie je pre mna jednoduche robit ).
Mas pravdu, ze klucove slovo je posunutie= translacia.... a to umoznuje napisat pedantnejsie navrhnutu konstrukciu ale to by bolo priliz pre bez neho stredoskolaka.
( Poznamka: co sa tyka indikacii na konstrukciu, co som napisal, je jasne, ze len jeden z dvoch bodov prieseku kruznice a ronobezky vyhovuje, ale vdaka urobenej analyze sa lahko urci).
Podla mna ide o zaujimave cvicenie, ktore je vhodne do nejake ho matematickeho kruzku alebo pre buduceho ucitela. ( Dufam, ze taketo cvicenia, sa necakaju od bezneho dnesneho ziaka .... vsak to ani dnesne osnovy necakaju...)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#24 14. 11. 2017 23:44
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Konstrukce 4úhelníku
↑ vanok:
Zdravím, opozděně děkuji za upřesnění,
abychom ukončili téma (předpokládám, že autorce tématu chodí oznámení mailem o novém příspěvku, tak to může upřesnit - kde úloha vznikla apod.). Užití posunutí v konstrukcích je snad pořad v běžném školním programu.
Ohledně náčrtu - na úvod pro rozbor situace zadání, tak určitě, ale jinak je "průkaznější" popis konstrukce. Zde popisujeme např. vznik průsečíků jednotlivých množin bodů určitých vlastností a lze tak ukázat, zda jdeme k řešení úlohy. V kreslicím programu (i ručně) se může podařit zvolit takové rozměry, že úloha se zda být vyřešena i nesprávnou metodou.
Pravda, že popis konstrukce vyžaduje symboly, tedy je snad obtížnější částí řešení, než samotný nápad na sestrojení.
Tak ještě počkáme na autorku tématu, zda dořešila. Pozdravy.
Offline