Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 10. 2017 13:14 — Editoval Zvedavec 4 (24. 10. 2017 13:54)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Vypocet "t'"
Je zajimave, ze valna vetsina vzorecku pouzitych v STR jsou zdanlive hodne jednoduche. Samozrejme je to pak jejich pojeti, nebo-li concept, ktery je pak vetsinou mnohem slozitejsi.
V priklade, kdy se udalost stane za 1 000 vterin ve vzdalenosti x=259 807 621.1km a kdy k ni raketa leti rychlosti v=259 807.621 1km/s.
Jelikoz t'=2(1 000 - 0.866 025 403 x 866.025 403) = 2(1 000 - 750)=500 vterin, znamena to, ze v okamziku, kdy se raketa nachazi v 750 vterinach tzv.souradnicoveho casu soustavy "v klidu"(Zeme), tedy to cislo 750 vterin v soustave rakety nefiguruje, svetelny paprsek se nachazi v miste budouci udalosti, tedy v 866 vterinach souradnicoveho casu Zeme, tedy dalsich 116 vterin, podle soustavy Zeme, letu pro tu raketu k te udalosti doletnout a svetlu potrva dalsich 134 vterin do pozadovanych 1 000 vterin.
Neni mi jasne, proc by se melo odecitat tech 750 vterin od celkoveho casu 1 000 vterin ubehleho na Zemi, kdyz spolu ty dva casy nemaji skoro nic spolecneho? 750 vterin je casem tzv.souradnicovym, kde se raketa nachazi v 866 vterinach casu ubehleho na Zemi, cili neni to ani cas ubehly na Zemi a ani cas rakety, jejiz ubehly cas v tom okamziku je nejspis 750/2=375 vterin.
Mohl by to nekdo trochu objasnit?
Offline
#2 25. 10. 2017 09:47
Re: Vypocet "t'"
↑ Zvedavec 4:
Nepřehlednost tvých příspěvků již delší dobu roste a teď už podle mého překročila jakékoli únosné meze. Velmi bych se divil, kdyby z tvého popisu někdo pochopil, o co ti jde. Buď si dej tu práci dotaz pořádně formulovat, nebo na něj nečekej odpověď.
Offline
#4 26. 10. 2017 13:21 — Editoval Zvedavec 4 (30. 10. 2017 01:22)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Vypocet "t'"
Omlouvam se za nejasnost meho dotazu, je to dost zamotany, jak sami uznate. Snad se mi to ted dari lip.
Kdyz si do vzorecku x'=gama(x-vt) a t'=gama(t-vx/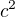 ) pro vypocet velicin v soustave "v pohybu" dosadim nejake konkretni hodnoty, kde vzdalenost v soustave "v klidu", tedy na Zemi, k urcite konkretni udalosti je x=259 807 621.1km, a kdy raketa k ni ma doletnout rychlosti v=259 807.621 1km/s, kdy gama=2, za dobu t=1 000 vterin.
) pro vypocet velicin v soustave "v pohybu" dosadim nejake konkretni hodnoty, kde vzdalenost v soustave "v klidu", tedy na Zemi, k urcite konkretni udalosti je x=259 807 621.1km, a kdy raketa k ni ma doletnout rychlosti v=259 807.621 1km/s, kdy gama=2, za dobu t=1 000 vterin.
V pripade vypoctu t'=gama(t-vx/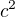 )=2(1000-259 807.621 1 x 259 807 621 1/
)=2(1000-259 807.621 1 x 259 807 621 1/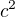 )=2(1000-0.866 025 403 x 866.025 403 8)=2(1000-750)=2(250)=500s.
)=2(1000-0.866 025 403 x 866.025 403 8)=2(1000-750)=2(250)=500s.
x' vyjde 0km. Predpokladam tedy, ze to znamena, ze udalost se stane v pocatku, tedy x=0, prostorove souradnice soustavy rakety, tedy soustavy "v pohybu", a v 500-ti vterinach v jeji casove souradnici, tedy t'=500 vterin.
Ta udalost se stane v miste vzdalenem 259 807 621.1km od nulove polohy soustavy "v klidu", tedy Zeme. V te soustave ta vzdalenost predstavuje tzv. souradnicovy cas 866.025 403 8-ti vterin. Raketa se ale v tu dobu, kdy se ta udalost stane, uz nenachazi v tzv. souradnicovem case 750 vterin, ale v tomhle samem souradnicovem case 866.025 403 8 vterin, kdy uz vlastne bude ubehlych 1000 vterin.
Neni mi jasny koncept, podle ktereho se tedy tech 750 vterin polohy rakety v okamziku, ve kterem uz vlastne ubehlo 866.025 403 8 vterin (hodnoty jak merene v soustave "v klidu"), jednoduse odecte od celkoveho casu 1000 vterin, ve kterem se ta udalost stane aby se ziskal cas t', tedy cas ubehly v soustave "v pohybu", tedy v soustave rakety, tedy t'=500 vterin.
Tech 1000 vterin je cas ubehly a tech 750 vterin je ten tzv. cas souradnicovy, ve kterem okamziku polohy rakety uz (ve skutecnosti soustavy "v klidu") ubehlo 866.025 403 8 vterin.
Nezda se to dost logicke odecist souradnicovy cas 750-ti vterin, kdy uz ve skutecnosti ubehlo 866.025 403 8 vterin, od casu ocekavaneho v budoucnosti, tedy 1000 vterin, kdy ta raketa bude v souradnicovem case 866.025 403 8 vterin, a ne v tech 750-ti vterinach, aby se dostal ubehly cas rakerty, tedy cas v soustave "v pohybu" .
Nenarazil jsem ani na castecny rozbor toho jak se k tomu vzorci doslo, ktery by snad vrhnul nejake svetlo na jeho logiku, a protoze neznam vsechny detajly STR a ani matematiky k ni potrebne a nevim, kde by mohla byt chyba v me uvaze, obracim na tohle forum.
Offline
#5 26. 10. 2017 15:29
Re: Vypocet "t'"
↑ Zvedavec 4:
No, je to delší, ale o moc jasnější ne. Evidentně jde tedy o situaci, kdy od Země letí raketa, která si v okamžiku míjení sesynchronizuje hodiny se Zemi a oba pozorovatelé si ty své nastaví na nulu. Událost, která z pohledu Země nastane v čase t=1000 sekund a na poloze x=259 807 621 km se z pohledu lodi stane přesně v okamžiku, kdy kolem příslušného místa prolétá (x'=0) a to po uplynutí 500 sekund (t'=500 s). Potud je vše v pořádku. Mimochodem, i pozorovatel na Zemi uvidí událost přesně ve chvíli, kdy tam poletí ta loď (jsou to soumístné události, takže jinak to nejde), akorát se to stane po uplynutí času 1000 s, přesně jak to bylo vymyšlené.
Zbytek tvého příspěvku je velmi zmatený a to především v tom, že střídáš používané jednotky času a vzdálenosti (což je přesně to, na co upozorňuje ↑ edison:). Ten "tzv. souřadnicový čas" je vzdálenost měřená ve světelných sekundách, což tam nakonec občas i píšeš, ovšem je to velmi nepřehledné. Pokud chceš měřit čas a vzdálenost ve stejných jednotkách, je to v pořádku (a také se to tak často dělá), ale pak se nikde nesmí objevovat žádné kilometry a rychlost světla c musí být bezrozměrná a rovná jedné. Nic z toho u tebe ale neplatí.
A skoro mi přijde, že přesně do toho ses zamotal sám. Píšeš totiž
Zvedavec 4 napsal(a):
Ta udalost se stane v miste vzdalenem 259 807 621.1km od nulove polohy soustavy "v klidu", tedy Zeme. V te soustave ta vzdalenost predstavuje tzv. souradnicovy cas 866.025 403 8-ti vterin. Raketa se ale v tu dobu, kdy se ta udalost stane, uz nachazi v tzv. souradnicovem case 750 vterin, ale v tomhle samem souradnicovem case 866.025 403 8 vterin, kdy uz vlastne bude ubehlych 1000 vterin.
Jediný způsob, jak se mi podařilo dostat 750 sekund bylo tak, že jsem vzal 866 sekund času při pohledu ze Země a podíval se, v jaké vzdálenost od Země v tu chvíli loď je. Pak vyjde vzdálenost 750 s. Problém je ovšem v tom, že v čase 866 s na Zemi ta loď ještě vůbec na místě události není. Což vyvrací to, co píšeš (nehledě k tomu, že to ani samo o sobě nedává dobrý smysl).
A není mi toho jasné víc, například
Zvedavec 4 napsal(a):
se tedy tech 750 vterin polohy rakety v okamziku, ve kterem uz vlastne ubehlo 866.025 403 8 vterin (hodnoty jak merene v soustave "v klidu"), jednoduse odecte od celkoveho casu 1000 vterin, ve kterem se ta udalost stane aby se ziskal cas t', tedy cas ubehly v soustave "v pohybu", tedy v soustave rakety, tedy t'=500 vterin.
Já nevím, ale když "jednoduše" odečtu 750 od 1000, tak dostanu 250, a ne 500.
Popravdě řečeno by možná bylo lepší, kdybys naopak skutečně používal SI jednotky (tedy km a s). Pak bys aspoň nemohl odčítat čas a vzdálenost, v čemž tady možná je zakopaný pes. Relativita je především o tom neplést dohromady veličiny z různých souřadnicových soustav. Mně přijde, že to nejenže děláš, ale díky změnám jednotek dokážeš smíchat i čas se vzdáleností. Pak opravdu může vyjít ledasco.
Ale jak říkám, nejsem si jistý, nakolik jsem to rozklíčoval správně. A ani mi není jasné, co se vlastně snažíš spočítat, zkontrolovat nebo vyvrátit.
Offline
#6 27. 10. 2017 13:41 — Editoval Zvedavec 4 (27. 10. 2017 13:53)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Vypocet "t'"
Dekuju za odpoved a musim se priznat, ze jsem si uvedomil, co to vlastne Edison pozadoval, az kdyz jsem se uz k pocitaci vratit nemohl abych to zmenil. Ale ted uz to je snad jedno, kdyz uz jsme uprostred.
Za prve, se tam nejak vloudila zavazna chyba a to, v:
LukasM napsal(a):
Zvedavec 4 napsal(a):
Ta udalost se stane v miste vzdalenem 259 807 621.1km od nulove polohy soustavy "v klidu", tedy Zeme. V te soustave ta vzdalenost predstavuje tzv. souradnicovy cas 866.025 403 8-ti vterin. Raketa se ale v tu dobu, kdy se ta udalost stane, uz nachazi v tzv. souradnicovem case 750 vterin, ale v tomhle samem souradnicovem case 866.025 403 8 vterin, kdy uz vlastne bude ubehlych 1000 vterin.
ma byt "....raketa se uz NEnachazi...."
Jde mi o koncept, jakym muzou dojit k zaveru, ze cas rakety je 500 vterin na zaklade tohoto vzorce, a to z duvodu, ze:
1) raketa se nachazi v 750-ti vterinach souradnyho casu v okamziku, kdy foton dorazil do 866 vterin souradneho casu, tedy kdy nasledne ubehly cas jak na Zemi, tak i v miste okamzite polohy rakety je 866 vterin.
2) raketa se nachazi v 866-ti vterinach souradneho casu, tedy v miste te udalosti v okamziku, kdy se foton nachazi v 1000-ci vterinach souradneho casu, kdy uplynuly cas jak na Zemi, tak v okamzite poloze rakety je 1000 vterin a tedy v okamziku, kdy se prave stava ta udalost.
Jelikoz tech 750 vterin casu souradneho byla minula pozice rakety a to v dobe 866 vterin casu uplynuleho, ale tech 1000 vterin souradneho casu nema s raketou zadne spojeni (toho mista v tomhle priklade nedosahne), avsak 1000 vterin casu uplynuleho s ni spojeni ma, protoze v tom case se nachazi v miste te udalosti.
Takze to vypada, ze odectenim 750-ti vterin souradneho casu soustavy "v klidu" polohy rakety od 1000-ce vterin casu uplynuleho soustavy "v klidu" nam da tech 250 vterin, ktere se pak vynasobi gamou s vysledkem 500-ti vterin uplynuleho casu rakety a to v jine, tedy jeji, soustave "v pohybu".
Co mi v tyhle uvaze nehraje je to, ze se tu zdanlive michaji "hodinky a holinky", jelikoz se od casu ubehleho, tedy konecneho 1000-ce vterin, odecita pozice rakety, tedy cas souradnicovy, tedy minula pozice rakety 750-ti vterin.
Vubec se to nesnazim vyvratit, jenom bych rad vedel jakou uvahou se pomoci tohoto vzorce doslo k tomu, ze uplynuly cas rakety v dobe udalosti bude tech 500 vterin.
Je to zamotany a tak se to da tezko popsat a je mozne, ze jsem to zbytecne zkomplikoval a nekde jsem neco dobre nepochopil.
Skratka 750 vterin (v km) souradneho casu polohy rakety, porotoze ubehlym casem 750-ti vterin v ramci tohodle prikladu neprolitala, se odecita (alespon zdanlive) od celkoveho ubehleho casu 1000-ce vterin.
Offline
#7 30. 10. 2017 00:57 — Editoval Zvedavec 4 (30. 10. 2017 10:58)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Vypocet "t'"
Asi nejjednoduzsim zpusobem jak to popsat je, ze ten priklad zacina v case 866 vterin. Jedinych 750 vterin co v nem figuruje muze jenom byt pozice rakety v ten samy okamzik, tedy kdy priklad zacina, tedy v case 866 vterin. Cili tech 750 vterin muze jenom znamenat cas souradny.
Na druhou stranu priklad konci v 1 000-ci vterinach, kdy se ta udalost stane. A tedy jedinych 1 000 vterin, co tam figuruje je doba udalosti v 1000-ci vterinach, tedy cas uplynuly.
A proto to jasne vypada, ze se tu odcita souradny cas od casu ubehleho. To si myslim by nemelo byt.
Jiny pohled na to muze byt, ze tech 1 000 vterin znaci cas souradny, tedy dolet fotonu, ktery je totozny s konecnym casem ubehlym a pak by to mohlo byt vporadku, protoze casem t' je, jak bych tomu rozumel, myslena pozice te udalosti v casove souradnici soustavy "v pohybu" a pak by se tedy odecitaly dva casy souradne.
Hodnoty v tomhle priklade jsou zavadejici v tom, ze ubehly cas rakety v jeji soustave, tedy 500 vterin v dobe udalosti, je ciselne totozny s casem souradnym t', ve kterem se ta udalost stane na jeji casove souradnici, tedy taky 500 vterin.
Nechci se primo ptat, jak je ten vzorec odvozeny, protoze nejsem matematik jenom jsem doufal, ze nekdo vysvetli pojeti nebo concept jak se k nemu doslo.
Jestli nekdo vi, proc se, konkretne v tomhle priklade, tech 750 vterin musi odecist od 1000-ce vterin aby se dostal cas t' anebo, kde je chyba v me uvaze, byl bych rad, kdyby to vysvetlil.
Offline
#8 30. 10. 2017 17:34 — Editoval KennyMcCormick (30. 10. 2017 17:46)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Vypocet "t'"
Číslovky psané čísly se neskloňují (píše se "750", "1000", ne "750-ti", "1000-ce"). :)
↑ Zvedavec 4:
Jde mi o koncept, jakym muzou dojit k zaveru, ze cas rakety je 500 vterin
A proto to jasne vypada, ze se tu odcita souradny cas od casu ubehleho. To si myslim by nemelo byt.
Každý souřadný čas je čas uběhlý.
Nechci se primo ptat, jak je ten vzorec odvozeny, protoze nejsem matematik jenom jsem doufal, ze nekdo vysvetli pojeti nebo concept jak se k nemu doslo.

Vynásobíme obě zelené strany rovnice výrazem  :
:
Roznásobíme a přesuneme dva členy na druhou stranu: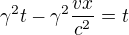
Vydělíme obě strany  a prohodíme je:
a prohodíme je: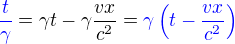
Protože , vidíme, že
, vidíme, že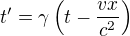 .
.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#9 07. 11. 2017 12:38 — Editoval Zvedavec 4 (07. 11. 2017 13:55)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Vypocet "t'"
↑ KennyMcCormick:
Kenny, dekuju za odpoved a ten pocetni rozbor. Kdyz ale mluvim o konceptu mam na mysli intuitivni koncept, ktery autor toho vzorecku, bud Einstein nebo Lorentz, musel mit na mysli, a ze ktereho ten vzorecek odvodil. Tak, jako si Einstein odvodil celou Teorii Relativity a jeji matematiku z konceptu se svetelnymi hodinami.
Protoze ten zakladni vzorecek t=x/v je hned na zacatku zmanipulovany tak, aby tam vzniknul ten pocetni vyraz 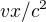 , tenhle pocetni vyraz se tedy zda byt tim hlavnim a puvodnim intuitivnim konceptem, ze ktereho se pak ten zbytek matematiky odvodil. To
, tenhle pocetni vyraz se tedy zda byt tim hlavnim a puvodnim intuitivnim konceptem, ze ktereho se pak ten zbytek matematiky odvodil. To 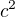 asi meni obycejny prostorovy vypocet t=x/v na vypocet casoprostorovy.
asi meni obycejny prostorovy vypocet t=x/v na vypocet casoprostorovy.
Protoze muj dotaz se ale tykal toho, jak se odectenim 750 of 1 000 muze odvodit to, ze rakete uplyne 500 vterin v dobe udalosti, sousttredil jsem se hlavne na to abych na to prisel. Z tveho rozboru jsem si zatim odvodil tohle (tedy odpoved, kterou jsem hledal):
Chyba v me uvaze byla, ze jsem bral v potaz jenom pohyp prostorem. Problemem tady je, ze ta udalost se nestane v pouhych 295 807 621,1 km prostoru, ale v 295 807 621,1 km a 1 000 vterinach casoprostoru. Tech 866 vterin, coby souradny cas mista udalosti, je tedy ciste prostorovy rozmer mereny ve vterinach.
Takze spravnejsi chapani toho vyrazu 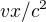 je, ze kazdou vterinu se prostorove souradnice Zeme a rakety sice posouvaji vuci sobe pomerem 0.866, ale jejich casove souradnice se vuci sobe posouvaji pomerem 0.75.
je, ze kazdou vterinu se prostorove souradnice Zeme a rakety sice posouvaji vuci sobe pomerem 0.866, ale jejich casove souradnice se vuci sobe posouvaji pomerem 0.75.
To znamena, ze v 1 000 vterinach uplynulych na Zemi, v okamziku kdy se ta udalost stane, se nula casove souradnice rakety bude nachazet v 750 vterinach casove souradnice Zeme, ale samotna raketa se bude, kvuli dilataci a kontrakci, nachazet uz v tech 1 000 vterinach casove souradnice Zeme, tedy v miste udalosti, a tudiz se ta udalost stane v miste spocitanych 250 vterin casove souradnice rakety (podle meritka Zeme).
Protoze ale prepoctovy pomer(faktor)gama=2 nam rika, ze se cas rakety pri tehle jeji rychlosti letu navic dilatuje 2-ma a jeji prostor se 2-ma krati, casova vzdalenost te udalosti od nuly casove souradnice rakety tedy bude ve skutecnosti 2x tech spocitanych 250 vterin, tedy 500 vterin (jak videno ze Zeme), tedy v polovine tech 1 000 vterin casu uplynuleho na Zemi a dvojnasobek tech 500 vterin (jak videnych na Zemi), tedy 1 000 vterin, odtikanych a videnych v rakete.
Snad se tady vyjadruju dost presne aby se dalo pochopit, co tim myslim.
Offline
#10 07. 11. 2017 16:17 — Editoval KennyMcCormick (07. 11. 2017 16:38)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Vypocet "t'"
Kdyz ale mluvim o konceptu mam na mysli intuitivni koncept, ktery autor toho vzorecku, bud Einstein nebo Lorentz, musel mit na mysli, a ze ktereho ten vzorecek odvodil.
Můžeš to odvodit z konceptu, že je to jediná rovnice kompatibilní s a
a .
.
jak se odectenim 750 of 1 000 muze odvodit to, ze rakete uplyne 500 vterin v dobe udalosti, sousttredil jsem se hlavne na to abych na to prisel
To se skládá ze 2 částí:
1. Odvodíš si vzoreček, do kterého dosazuješ.
2. Dosadíš do vzorečku.
To
asi meni obycejny prostorovy vypocet t=x/v na vypocet casoprostorovy.
Já třeba nevím, jaký je rozdíl mezi prostorovým a časoprostorovým výpočtem.
Takze spravnejsi chapani toho vyrazu
je, ze kazdou vterinu se prostorove souradnice Zeme a rakety sice posouvaji vuci sobe pomerem 0.866, ale jejich casove souradnice se vuci sobe posouvaji pomerem 0.75.
Co je to poměr souřadnic?
se nula casove souradnice rakety bude nachazet v 750 vterinach casove souradnice Zeme
Co to znamená?
2-ma
"2", bez "-ma". :)
tedy 1 000 vterin, odtikanych a videnych v rakete
Co znamená tohle?
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#11 10. 11. 2017 13:15 — Editoval Zvedavec 4 (11. 11. 2017 00:39)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Vypocet "t'"
Kenny, dekuju za odpoved.
Ty to vidis z ciste matematickeho hlediska. Ja se tomu snnazim porozumnet hlavne z hlediska intuitivniho. Nektere vzorecky jsou pro mne dulezity, ale spis druhotny pokud mi nepomuzou utvorit si jejich pomoci koncept o cem jsou.
Podle meho, Einstein musel nejdriv mit nejaky, co bych nazval, intuitivni koncept, ktery potom vyjadril nebo "zasifroval" do pocetnich vzorcu. Nematematik je musi "rozsifrovat" zpatky do intuitivniho konceptu aby tomu dobre rozumnel, protoze nezname vsechny triky matematiky, a to hlavne asi algebry, aby nam sama o sobe mohla veci uplne vyjasnit.
KennyMcCormick napsal(a):
To
asi meni obycejny prostorovy vypocet t=x/v na vypocet casoprostorovy.
Já třeba nevím, jaký je rozdíl mezi prostorovým a časoprostorovým výpočtem.
Nez jsem si uvedomil, ze se jedna o pohyb casoprostorem,
=750 vterin pro mne znamenalo, ze protoze se raketa v case 866 vterin, tedy v case pred tou udalosti, nachazi v 750 vterinach souradnyho casu, tedy v ciste prostorove vzdalenosti od startu, odecist je od 1 000 vterin odtikanych v dobe udalosti nedava smysl, protoze ty dva casy nejsou spolu nijak spojeny, protoze v te dobe, kdy se raketa nachazi v tech 750 vterinach souradneho casu, je cas 866 vterin a tedy pozice rakety se nezda byt dulezita. Prestoze tech 750 vterin je nejenom mistem v km, ale taky casem ve vterinach, je to casem pred zacatkem toho prikladu, ktery zacina v 866 vterinach. Co ma pozice rakety v nejakem libovolnem okamziku anebo cas uplynuly pred zacatkem toho prikladu, spolecneho s konecnym casem toho prikladu, kdy se ta udalost stane? To byla ma otazka.
Ale protoze se raketa taky premistuje po ose casove tech 750 vterin je pak casem, ve kterem se pocatek jeji casove souradnice nachazi v dobe zacatku toho prikladu, tedy v ubehlem case 866 vterin a tudiz ji schazi na konecnou pozici fotonu 250 vterin, tedy doba, ktera nam po vynasobeni gamou da polohu te udalosti v casove souradnici rakety a to je, jak bych tomu rozumnel, ucel toho vzorecku, tedy to "t'".Takze spravnejsi chapani toho vyrazu
je, ze kazdou vterinu se prostorove souradnice Zeme a rakety sice posouvaji vuci sobe pomerem 0.866, ale jejich casove souradnice se vuci sobe posouvaji pomerem 0.75.
Co je to poměr souřadnic?
Asi to neni nejlepsi vyraz, jak to popsat, ale rozumim tomu tak, ze ucelem toho vypoctu je ukazat, o kolik se ty dvoje souradnice Zeme a rakety, tedy prostorova a casova, premistovanim soustavy "v pohybu", tedy letem rakety, vuci sobe posouvaji. V tomhle priklade se prostorove souradnice vuci sobe vychili o 86(nebo mozna spis14)% a casove o 75(nebo mozna spis 25)%, kde raketa se nachazi v 750 vterinach, tedy v 75% z 1 000 vterin.
se nula casove souradnice rakety bude nachazet v 750 vterinach casove souradnice Zeme
Co to znamená?
Jestlize se ta raketa nachazi v miste udalosti, tak aby se ta udalost stala v jejich 2x250=500 vterinach, tedy v 500 vterinach na jeji casove souradnici, musi se pocatek jeji casove souradnice kryt se 750 vterinami casove souradnice Zeme.
A taky tohle je to, co si je treba, jak bych to chapal ted, intuitivne uvedomit.
Offline
#12 10. 11. 2017 15:12
Re: Vypocet "t'"
Zvedavec 4 napsal(a):
Podle meho, Einstein musel nejdriv mit nejaky, co bych nazval, intuitivni koncept, ktery potom vyjadril nebo "zasifroval" do pocetnich vzorcu.
Ano, ten intuitivní koncept se jmenuje postuláty speciální relativity. To je slovní vyjádření podmínek, které musí pohybové zákony splňovat, aby byly v souladu s Maxwellovými rovnicemi.
Offline
#13 11. 11. 2017 00:50 — Editoval Zvedavec 4 (11. 11. 2017 00:53)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Vypocet "t'"
Ano, ten intuitivní koncept se jmenuje postuláty speciální relativity. To je slovní vyjádření podmínek, které musí pohybové zákony splňovat, aby byly v souladu s Maxwellovými rovnicemi.
To je vlastne asi ten druhy zpusob. Tedy uz zname vedecke objevy a zformulovane pocetni vzorce, ktere je popisuji, pak daji podnet k nejakemu vyssimu konceptu, ktery vysvetli do te doby neporozumneny ukaz, jako ty Maxwellovy rovnice, ktere snad byly mezi duvody, proc si Einstein utvoril koncept Teorie Relativity. Ale i ty puvodni vzorce musely jenom popisovat nejaky pocatecni koncept.
Offline
#14 13. 11. 2017 07:15 — Editoval LukasM (13. 11. 2017 07:16)
Re: Vypocet "t'"
↑ Zvedavec 4:
Já mám trochu pocit, že pokusy pochopit speciální relativitu zaměřuješ naprosto nevhodným směrem. V jednom z vedlejších vláken ses snažil ve všem vidět hyperboly, a když tam nebyly, tak alespoň podobně zahnuté křivky. Nyní je tvým svatým grálem "počáteční koncept", aniž bys vysvětlil (a možná sám věděl), co to vlastně má být.
Zvedavec 4 napsal(a):
...vzorce. Nematematik je musi "rozsifrovat" zpatky do intuitivniho konceptu aby tomu dobre rozumnel, protoze nezname vsechny triky matematiky, a to hlavne asi algebry, aby nam sama o sobe mohla veci uplne vyjasnit.
Tohle je možná ten problém. Smiř se s tím, že fyzikální teorie jsou zpravidla vyjádřeny jazykem matematiky. Takže je potřeba ji alespoň základně ovládat. Zrovna pro STR, tak jak tu o ní mluvíme my, není žádná složitá matematika potřeba, v podstatě stačí věci ze ZŠ. Takže bych ten matematický popis nezatracoval, může se totiž stát, že to intuitivně pochopit nepůjde.
Zvedavec 4 napsal(a):
uz zname vedecke objevy a zformulovane pocetni vzorce, ktere je popisuji, pak daji podnet
Ale tak to je vždycky. Lidské poznání se postupně nabaluje, není žádná ostuda, že Einstein v době psaní už o fyzice něco věděl a svou teorii vytvořil tak, aby s tím byla v souladu (resp. dokonce vyřešila nějaké rozpory, které tam do té doby byly). Tak hluboké zákony, jako je STR nejdou vymyslet tak, že pračlověk seskočí ze stromu a vyryje je klackem do bláta, protože ho osvítil "koncept". Zdá se mi, že v tom hledáš nějaké filozofično, které tam nejspíš vůbec není.
Offline
#15 13. 11. 2017 17:55 — Editoval Zvedavec 4 (13. 11. 2017 18:15)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Vypocet "t'"
↑ LukasM: Musim souhlasit. Ale jelikoz jsem rad, ze jsem ten pocetni vyraz 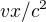 konecne rozlustil a tedy tim svou puvodni otazku tohoto vlakna, posilam to pochopeni do tohoto fora k posouzeni. Vim, ze je to dobre, i kdyz mozna tezko nekdo pochopi, co tim myslim. Urcite v nem jsou technicke nepresnosti, ale princip, verim, je v poradku.
konecne rozlustil a tedy tim svou puvodni otazku tohoto vlakna, posilam to pochopeni do tohoto fora k posouzeni. Vim, ze je to dobre, i kdyz mozna tezko nekdo pochopi, co tim myslim. Urcite v nem jsou technicke nepresnosti, ale princip, verim, je v poradku.
Na diagramu, svisla primka bude predstavovat souradnici ciste casovou "t" a k ni kolma vodorovna primka bude predstavovat souradnici ciste prostorovou "x".
Souradnice "t" tedy predstavuje plynuti casu teles "v klidu", kde intervaly na ni jsou ve vterinach.
Souradnice "x" predstavuje letovou drahu fotonu, ktery jediny se muze pohybovat ciste prostorove, a muze se usuzovat, ze predstavuje tedy taky plynuti casu pro telesa "v pohybu" porovnanim jejich vzdalenosti doletu v km nebo souradnych vterinach se vzdalenosti doletu fotonu coby nositele casu, jak se zda z tohodle prikladu.
To znamena, ze pohybova draha jakehokoli telesa "v pohybu" muze nasledovat jenom uhlopricku v prostoru vymezenem tema dvema souradnicema a ty uhlopricky mohou predstavovat jedine souradnice casoprostoru, taky proto, ze slucuji pohyb casem a prostorem.
Letova draha rakety tedy bude muset byt nejak odklonena, konceptualne, od osy "x" a to uhlem neprimo umernym jeji rychlosti. Ta jeji letova draha bude muset byt jeji casoprostorovou (casovou a prostorovou soucasne) souradnici.
Udalost, ke ktere ta raketa smeruje se tedy bude muset nachazet na jeji casoprostorove souradnici, tedy na jeji draze letu a ne na ose "x".
Z hlediska rakety, je misto te udalosti, v predpokladu kosmonautu, vzdaleno 259 807 621.1 km, tedy 866 souradnych vterin, na teto jeji souradnici a z hlediska pozorovatele na Zemi je to misto udalosti taky vzdaleno tech 259 807 621.1 km, tedy 866 souradnych vterin, ale na ose "x" Zeme, po niz tedy ta raketa zdanlive, z hlediska Zeme, leti.
Raketa bude muset byt v miste udalosti, podle vypoctu, tedy v 866 souradnych vterinach, v case 1 000 uplynulych vterin jak z hlediska Zeme tak z hlediska rakety.
Kdyz pozorovatel na Zemi uvidi, ze raketa dorazila k te udalosti, tedy do 866 souradnych vterin, ve spravnem case 1 000 vterin (at souradnych nebo ubehlych), ty dva udaje nemuzou, coby intervaly na souradnici, lezet na stejne primce, protoze jsou ciselne rozilne, ale stanou se soucasne.
Kdyz foton dorazil do 1 000 vterin na sve ose "x" uplynulo tim 1 000 vterin casu na Zemi, a tedy z toho hlediska, tech 866 spocitanych souradnych vterin musi lezet na letove draze rakety, tedy jeji casoprostorove souradnici.
Pro pozorovatele v kazde z tech obou soustav, ciste prostorova souradnice muze jenom byt drahou fotonu, od ktere musi byt draha letu rakety nejak, konceptualne, odklonena.
Kdyz tedy z hlediska Zeme, 866 souradnych vterin rakety se deje v okamziku, kdy foton dorazil do 1 000 vterin osy "x", v/c musi znamenat, ze tech 866 souradnych vterin je umisteno na letove draze rakety a musi se promitnout na osu "x" aby se dostalo tech vzorcem pozadovanych 750 vterin, ktere se teprve, protoze oba ty udaje, 1000 a 750 vterin, ted lezi na stejne primce, muzou od sebe primo odecist a dostat tak spocitanych 250 vterin. 250 vterin vynasobenych gamou nam da misto udalosti na casove souradnici rakety. A to je ucel celeho vzorecku pro vypocet t'.
Ciselne hodnoty jsou z pohledu pozorovatele na Zemi, jak se deji na rakete a jeji letove draze. Z pohledu rakety to bude nejak relativisticky obracene.
Offline
#16 21. 11. 2017 13:08 — Editoval Zvedavec 4 (21. 11. 2017 13:15)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Vypocet "t'"
Kenny, bohuzel jsem zapomnel vetsinu stredoskolske algebry a tak mi neni jasne, jak se  promeni na
promeni na 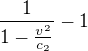 , i kdyz si nejak matne vzpominam, ze umistenim vyrazu do jmenovatele se ta jednicka nejak vytvori.
, i kdyz si nejak matne vzpominam, ze umistenim vyrazu do jmenovatele se ta jednicka nejak vytvori.
Protoze 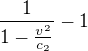 =3 a
=3 a  =0.3, kdyz si dosadim cisla, asi to tak bude. Ale utvrdil jsem se znovu v domence, pokud to nekdo nevyvrati, ze se vzorec pro vypocet gamy sklada z rafinovane zamaskovane Pythagorovy vety, kde se neustale zamenuji strany tim, ze se scitaji a odcitaji atd., protoze rozbor vrcholi jasnym
=0.3, kdyz si dosadim cisla, asi to tak bude. Ale utvrdil jsem se znovu v domence, pokud to nekdo nevyvrati, ze se vzorec pro vypocet gamy sklada z rafinovane zamaskovane Pythagorovy vety, kde se neustale zamenuji strany tim, ze se scitaji a odcitaji atd., protoze rozbor vrcholi jasnym 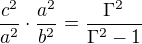
Jde o to, ze autor toho vzorecku pro 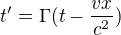 musel mit uz jasno, tedy prijit v mysli s konceptem, nejenom toho, ceho chce docilit, tedy vytvoreni vzorecku pro t', ale hlavne jeho ucelem ( toho t'). Taky mu byl uz uplne jasny koncept a ucel prepoctu gama.
musel mit uz jasno, tedy prijit v mysli s konceptem, nejenom toho, ceho chce docilit, tedy vytvoreni vzorecku pro t', ale hlavne jeho ucelem ( toho t'). Taky mu byl uz uplne jasny koncept a ucel prepoctu gama.
I ty zdanlive zapeklity koncepty STR, kdyz se je podari pochopit, se pak zdaji jednoduzsi az i elementalni, tedy skoro intuitivni. A o to mi jde.
Muj posledni popis toho, jak rozumet tomu prikladu a tedy vzorecku pro t' intuitivne nebyl moc jasny, ted kdyz si to znovu procitam.
Mel jsem na mysli to, ze fotonu cas neplyne, ale jeho pohyb, v pojeti STR, ho zpusobuje.
A tedy, kdyz se rekne, ze uplynulo 1 000 vterin, znamena to, ze se foton premistil po sve letove draze osy "x" do mista "X" vzdalenem 1 000 souradnych vterin a 300 000 000 km od startu. Zadne teleso se tedy nemuze nachazet v tom samem miste v tu samou dobu a to znamena, ze zadne teleso se nemuze premistovat po stejne draze letu (konceptualne).
Takze letova draha jakehokoliv telesa musi byt (konceptualne) jina, nez letova draha fotonu. A tedy nejak "odklonena".
Protoze na ose "x" 1 000 souradnych vterin znamena 1 000 uplynulych vterin, 866 souradnych vterin pak znamena pouhych 866 uplynulych vterin, tedy by znamenalo minulost.
Protoze se udalost, ktera se stane v miste s pouhymi 866 souradnymi vterinami se ma stat v case 1 000 vterin uplynulych na Zemi, nenachazi se v miste se stejnym souradnym casem jako ten foton, co tech 1 000 uplynulych vterin zpusobil, tudiz raketa, co k ni doletela za tech 1 000 vterin a tim preklenula vzdalenost pouhych 866 souradnych vterin, nemohla letet po stejne letove draze, jako ten foton. Kdyby letela, nachazela by se v minulosti, protoze v pritomnosti (ve skutecnosti) te drahy (soustavy fotonu) uz uplynulo 1 000 vterin. Proto musela jasne letet po jine draze, tedy v jine soustave, (konceptualne), i kdyz to muze vypadat, z hlediska pozorovatele na Zemi, ze letela. Ale jelikoz letela casoprostorem muze se nachazet soucasne v miste te udalosti vzdalenem pouhych 866 souradncyh vterin a v uplynulem case 1 000 vterin.
Jinymi slovy, kdyz tedy z hlediska Zeme, 866 souradnych vterin, kde se ta udalost stane, se uda v okamziku, kdy foton dorazil do 1 000 souradnych vterin osy "x", v/c musi znamenat jenom to, ze tech 866 souradnych vterin je umisteno na casoprostorove letove draze rakety a musi se promitnout na ciste prostorovou osu "x", tedy letovou drahu fotonu, aby se dostalo tech spocitanych 750 vterin a aby se daly nejak srovnavat s ubehlym casem 1000 vterin, tedy s umistenim fotonu.
Offline
#17 21. 11. 2017 22:53 — Editoval KennyMcCormick (21. 11. 2017 23:42)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Vypocet "t'"
Kenny, bohuzel jsem zapomnel vetsinu stredoskolske algebry a tak mi neni jasne, jak se
promeni na
Nepromění.
Jak se tam dostaneme?
Chceme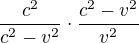 upravit na
upravit na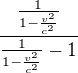 .
.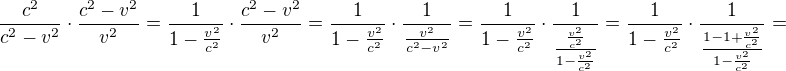
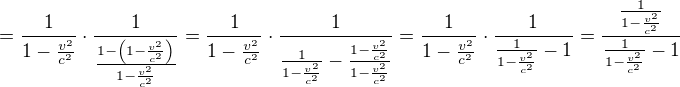
A je to.
Mel jsem na mysli to, ze fotonu cas neplyne, ale jeho pohyb, v pojeti STR, ho zpusobuje.
Co způsobuje?
(soustavy fotonu)
Foton nemá soustavu.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#18 23. 11. 2017 15:45 — Editoval Zvedavec 4 (23. 11. 2017 15:47)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Vypocet "t'"
Kenny, diky za ten bajecny rozbor. Neni to parada, ze se v matematice daji vzorecky takhle "zmanipulovat" a dostat pozadovany vysledek? Vlastne v podobnem duchu jsem byl schopen odhalit tu Pythagorovu vetu, i kdyz takhle daledko bych to rozebrat nedokazal. Pocty a matematiku jsem ve skole mival rad, a proto takovyhle rozbory porad jeste muzu alespon trochu nejak ocenit.
Ale takhle to manipulovat se muze jenom s konkretnim konceptem na mysli, ceho se chce docilit. Autor uz vedel, napriklad v tvym prvnim rozboru, ze  , a chtel tedy odvodit na tom zaklade ten rozsireny vzorec.
, a chtel tedy odvodit na tom zaklade ten rozsireny vzorec.
KennyMcCormick napsal(a):
Mel jsem na mysli to, ze fotonu cas neplyne, ale jeho pohyb, v pojeti STR, ho zpusobuje.
Co způsobuje?.
Neni to zname, ze aby se v STR zachovala stala "c" v ruznych soustavach, musi se menit jejich rychlost plynusti casu? A nejsou proto pohyb fotonu, coby ta "c", a rychlost plynuti casu tedy uzce propojene a tedy, v pojeti STR, totozne? Takze neni pak pohyb fotonu, kdyz se bere coby "c", v takovem pojeti, pricinou plynuti casu?
KennyMcCormick napsal(a):
(soustavy fotonu)
Foton nemá soustavu.
Soustavou fotonu jsem myslel pritomnost, kterou by ta raketa, kdyby letela po ciste prostorove ose nemohla dosahnout a ocitla by se tim padem v minulosti a ne v soucasnych 1 000 vterinach, ve kterych se ta udalost ma stat.
Offline
#19 23. 11. 2017 22:11 — Editoval Zvedavec 4 (23. 11. 2017 23:44)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Vypocet "t'"
Ten tvuj prvni rozbor ukazuje postup, jak je ten vzorecek 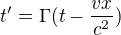 odvozenej. V tom zacatecnim
odvozenej. V tom zacatecnim  je tedy obsazen koncept P.vety, na ktere je to zalozene, a ktery je potom rozvedeny do detajlu a v tom
je tedy obsazen koncept P.vety, na ktere je to zalozene, a ktery je potom rozvedeny do detajlu a v tom  konceptem tedy je vztah mezi tema dvema soustavama, kterych se to tyka, tedy prevody mezi jejich souradnicema. Je to ted jasnejsi.
konceptem tedy je vztah mezi tema dvema soustavama, kterych se to tyka, tedy prevody mezi jejich souradnicema. Je to ted jasnejsi.
Vic uz z toho ale nevytezim a tak to nechci dal rozebirat a vracim se ke svemu puvodnimu dotazu.
Neni mi jasno, proc to vypada, ze ztotoznujes vzorecky  s
s  . To, ze v tom puvodnim priklade vyjdou obe hodnoty stejne je totiz zavadejici, jak tomu rozumim, a je to jenom kvuli pouzitym hodnotam. Kdyby tedy
. To, ze v tom puvodnim priklade vyjdou obe hodnoty stejne je totiz zavadejici, jak tomu rozumim, a je to jenom kvuli pouzitym hodnotam. Kdyby tedy 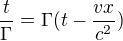 , ta druha cast, tedy
, ta druha cast, tedy  , by byla nejak navic. Ale spis musi mit nejaky ucel.
, by byla nejak navic. Ale spis musi mit nejaky ucel.
Kdyz si dosadim hodnoty v=259 807.621 1km/s, t=1 000s, x=100 km a Gama=2, vyjdou ty dva casy uplne rozdilne, takze 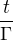 se jasne nerovna
se jasne nerovna  .
.
Memu chapani ten prvni vyjadruje jasne dilataci casu v soustave "v pohybu" zatimco ten druhy, jak se zdaji tvrdit na wiki, umisteni popsane udalosti v souradnicich te same soustavy. Takze ty dva casy oznacene stejne, tedy  , spolu nemaji nic spolecneho.
, spolu nemaji nic spolecneho.
Je mozne, ze se to neda pocitat pomoci tohodle vzorecku z STR, protoze mi je znamo, ze jakmile teleso zatoci, jedna se o OTR. Nicmene bylo receno, ze v tomhle priklade raketa musi letet obklikou (tedy musi zatocit) aby do udalosti doletla vcas, takze to budi dojem, ze by priklad s temito hodnotami ve spojeni s timhle vzorcem nejaky smysl davat mel.
Nevim, jestli prave tohle mely ty tvoje rozbory objasnit a jestli jo, tak jsem to z toho nevytezil.
Muzes to jeste nejak okomentovat?
Offline
#20 23. 11. 2017 23:16 Příspěvek uživatele KennyMcCormick byl skryt uživatelem KennyMcCormick.
#21 23. 11. 2017 23:24 — Editoval KennyMcCormick (24. 11. 2017 20:11)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Vypocet "t'"
A nejsou proto pohyb fotonu, coby ta "c", a rychlost plynuti casu tedy uzce propojene a tedy, v pojeti STR, totozne?
Tahle věta nedává smysl.
Fráze "pohyb fotonu" znamená, se existuje foton, který se pohybuje.
Foton má určitou rychlost, která je rovna  .
.
Ale všechny relativistické efekty by byly úplně stejné, i kdyby žádné fotony neexistovaly. Relativistické efekty jsou způsobené relativním pohybem daného tělesa (např. rakety) vůči pozorovateli. Vůbec nesouvisí s tím, jestli existují fotony a jestli se pohybují.
↑ Zvedavec 4:
To, ze v tom puvodnim priklade vyjdou obe hodnoty stejne je totiz zavadejici, jak tomu rozumim, a je to jenom kvuli pouzitym hodnotam.
Ty hodnoty vyjdou vždycky stejně.
Kdyz si dosadim hodnoty v=259 807.621 1km/s, t=1 000s, x=100 km a Gama=2
To nemůžeš (EDIT: Jsem pako: http://forum.matweb.cz/viewtopic.ph … 24#p555224), protože  je rychlost tělesa,
je rychlost tělesa,  je čas a
je čas a  je vzdálenost uražená tělesem.
je vzdálenost uražená tělesem.
Nemůžeš urazit 100 km rychlostí 259 807.621 1 km/s za 1 000 sekund.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#22 24. 11. 2017 00:47
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Vypocet "t'"
↑ KennyMcCormick:
Memu porozumneni, vsechny relativisticke efekty jsou zavisle prave na stale rychlosti "c", tedy pohybu fotonu. Efekty vzajemnych pohybu soustav jsou prave zpusobeny tim, ze jakoby v jejich pozadi, je "c" nemenna.
Muzu prece letet ohromnou obklikou abych dorazil do mista udalosti v pravy okamzik. V tom si myslim, je ten trik aby se ukazal ucel vzorecku pro vypocet t'. Proc by jinak popisovali na wiki jeho ucel tak, jak jsem se o nem zminil?
Offline
#23 24. 11. 2017 00:52
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Vypocet "t'"
Svuj predposledni prispevek (krom tohoto, tedy treti odsud) )jsem nekolikrat zeditoval a tak zpusobil zmatek v tom, co jsem tam vlastne napsal. Ale chtel jsem napsat to, co tam ted stoji.
Offline
#24 24. 11. 2017 01:06
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Vypocet "t'"
KennyMcCormick napsal(a):
Kdyz si dosadim hodnoty v=259 807.621 1km/s, t=1 000s, x=100 km a Gama=2
To nemůžeš, protože
je rychlost tělesa,
je čas a
je vzdálenost uražená tělesem.
Nemůžeš urazit 100 km rychlostí 259 807.621 1 km/s za 1 000 sekund.
Vidim, co chces rict, ale nepta se ten priklad prave na to, kde bude ta udalost umistena prave v souradnicich pohybujici se soustavy, tedy te rakety po tom, co doleti do mista udalosti jakoukoli rychlosti a obklikou?
Offline
#25 24. 11. 2017 01:53
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Vypocet "t'"
KennyMcCormick napsal(a):
To, ze v tom puvodnim priklade vyjdou obe hodnoty stejne je totiz zavadejici, jak tomu rozumim, a je to jenom kvuli pouzitym hodnotam.
Ty hodnoty vyjdou vždycky stejně.
Kdyz si dosadim hodnoty v=259 807.621 1km/s, t=1 000s, x=100 km a Gama=2
To nemůžeš, protože
je rychlost tělesa,
je čas a
je vzdálenost uražená tělesem.
Nemůžeš urazit 100 km rychlostí 259 807.621 1 km/s za 1 000 sekund.
Nevidim ucel v tom aby byly dva rozdilne vzorecky pro vypocet t' a oba vzdycky davaly totozny vysledek. Predpokladal bych, ze ucel toho vetsiho musi byt jiny a to takovy, jaky je popsany na wiki. Jinak to nedava smysl. Cely ten rozbor, cos tu popsal, by tomu taky nasvedcoval.
Melo by tady jit tedy o to, ze kdyz za 1 000 vterin se ta udalost stane ve 100km soustavy "v klidu", souradnice soustavy "v pohybu" budou cist  , minus, protoze ta raketa to misto zdaleka preletela, a
, minus, protoze ta raketa to misto zdaleka preletela, a  z toho sameho duvodu.
z toho sameho duvodu.
Tedy  popisuje dilataci a
popisuje dilataci a  pak popisuje vztah mezi soustavami ve vzajemnem pohybu v tom, kde se bude udalost nachazet v te druhe oproti te prvni. Ze jsou obe ve vzajemnem pohybu pak tedy vyzaduje aby to
pak popisuje vztah mezi soustavami ve vzajemnem pohybu v tom, kde se bude udalost nachazet v te druhe oproti te prvni. Ze jsou obe ve vzajemnem pohybu pak tedy vyzaduje aby to 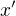 a
a  vzdycky popisovaly umisteni v souradnicich te druhe.
vzdycky popisovaly umisteni v souradnicich te druhe.
Takhle bych tomu rozumnel a zda se mi to davat smysl. Budu to muset na te wiki znovu najit, mozna si to spatne pamatuju anebo jsem si to spatne precet nebo nespravne pochopil.
Offline