Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 10. 2017 19:12 — Editoval liamlim (27. 10. 2017 20:09)
Axiom extenzionality
Zdravím všechny.
Tak jsem si trochu hrál s teorií množin a narazil jsem na jakýsi blok v mém pochopení dané věci. Prosím o potvrzení, že všechny myšlenky jsou správné. Některé úvahy mi připadají totiž dost podivné a nejsem si jistý, jestli axiom umožňuje všechny kroky, které provádím. Díky :)
Axiom extenzionality: 
Toto tvrzení platí speciálně pro 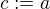 . Platí tedy:
. Platí tedy: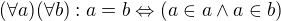
Platí ale i pro 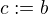 . Tedy:
. Tedy:
Dohromady tato dvě tvrzení z tranzitivity ekvivalence dávají:
Toto tvrzení musí platit speciálně pro  . Pak dostaneme:
. Pak dostaneme: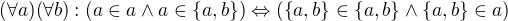
Přitom triválně platí 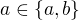 , proto se předchozí tvrzení zjednoduší:
, proto se předchozí tvrzení zjednoduší: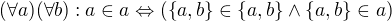
To specálně dává následující tvrzení:
1)  .
.
2) 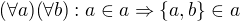
Tvrzení (1) platí speciálně pro  . Pak dostaneme
. Pak dostaneme 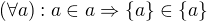 . Z definice
. Z definice 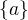 existuje jediná množina, která je v ní obsažena. Zároveň ale triviálně
existuje jediná množina, která je v ní obsažena. Zároveň ale triviálně  . To dohromady dává
. To dohromady dává
3)  .
.
Tohoto vztahu využijeme při úpravě (2). Tím dostaneme: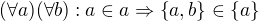 . Přitom ale na pravé straně je jednoprvková množina. Proto nutně
. Přitom ale na pravé straně je jednoprvková množina. Proto nutně  . Dohromady tedy máme:
. Dohromady tedy máme:
Neboli jestliže máme množinu, která obsahuje sama sebe, pak je nutně rovna úplně všem existujícím množinám. Existuje tedy jen jediná množina a ta navíc obsahuje sama sebe. To podle mého názoru vyvrací možnost existence takové množiny, nepletu se? Tvrzení 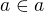 by prostě odpovídalo nepravdě.
by prostě odpovídalo nepravdě.
Proto nerozumím, kde je vlastně spor v tom, že by  . To je ekvivalentní zápisu
. To je ekvivalentní zápisu 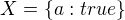 . Tedy by to byla množina všech množin. Přitom
. Tedy by to byla množina všech množin. Přitom 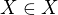 by bylo
by bylo  . Nestačilo by pro potlačení celého paradoxu prostě a jednoduše říct, že zápis
. Nestačilo by pro potlačení celého paradoxu prostě a jednoduše říct, že zápis  vlastně znamená:
vlastně znamená:  ? Tedy že vždy vybíráme z množiny všech množin... Díky za jakýkoliv názor..
? Tedy že vždy vybíráme z množiny všech množin... Díky za jakýkoliv názor..
Edit: Podle mě je toto úplně OK. Nepodařilo se mi dojít k žádnému sporu, pokud by platilo například 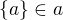 . Proto by klidně mohlo dle mého názoru třeba
. Proto by klidně mohlo dle mého názoru třeba 
Edit2: Teď jsem si všiml, že jsem si axiom extenzionality pamatoval trochu špatně. Navíc už mi připadají některé mé kroky vyloženě divné a chybné. Prosím o upozornění. Díky.
Offline
#2 27. 10. 2017 19:38 — Editoval liamlim (27. 10. 2017 20:01)
Re: Axiom extenzionality
To znamená tvrdím, že následující teorie množin by mohla být celkem fajn:
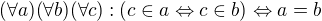
 => pojmenujeme
=> pojmenujeme 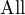

edit: Ten první axiom si nejsem jistý, jestli by byl vůbec třeba. Já jej využil v důkazu, že samotná extenzionalita vyvrací možnost 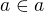 . Třetím axiomem si takovou možnost efektivně zakážu, neboť jediný možný kandidát na takovou množinu by byl
. Třetím axiomem si takovou možnost efektivně zakážu, neboť jediný možný kandidát na takovou množinu by byl 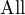 . Navíc jsem si jistý, že by první axiom bylo možno odvodit z axiomu vydělení
. Navíc jsem si jistý, že by první axiom bylo možno odvodit z axiomu vydělení
edit: možná by se slušelo zakázat teorii mající pouze množinu 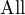 , která by obsahovala sama sebe přidáním axiomu:
, která by obsahovala sama sebe přidáním axiomu: 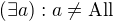
edit: Teď jsem zjistil, že třetí axiom sice nedefinuje 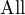 jednoznačně, ale že jsou si všechny izomorfní. Prostě je úplně jedno, kterou ze všech množin splňujících axiom 3 vybereme...
jednoznačně, ale že jsou si všechny izomorfní. Prostě je úplně jedno, kterou ze všech množin splňujících axiom 3 vybereme...
Offline
#3 27. 10. 2017 22:23 — Editoval Wotton (27. 10. 2017 22:26)
Re: Axiom extenzionality
↑ liamlim:
Ahoj,
nekoukal jsem na to dopodrobna, ale už to první tvrzení, které označuješ jako Axiom extenzionality je zjevně nepravdivé.
EDIT: za předpokladu standardního použití relací  a
a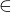
Dva jsou tisíckrát jeden.
Offline
