Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 06. 2009 00:56
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Definice výroku
Dobrý pozdní večer,
procházím si skripta a hned na začátku tématu jsem ustrnul. Píše se v nich: "Příkladem pravdivého výroku je výrok '2 < 3'."
Musel jsem se ihned podívat na nějaký webový zdroj (nepříliš věrohodná wikipedia mi potvrdila, že toto je výrok) - problémem je, že na střední škole jsme se vždy učili, že výrok může být pouze oznamovací věta a zapsání matematickými značkami nestačí.
Z toho tedy plyne má otázka: Jedná se o neznalost učitelů, úmyslné omezení středoškolské látky, nebo něco ještě odlišného?
Já jen doufám, že se nebudu "přeučovat" více takovýchto středoškolských záležitostí.
Otázka na vás: jak to bylo podáno vám? [na střední škole]
Díky
Offline
#2 26. 06. 2009 01:22
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Definice výroku
Já si pamatuju toto:
Výrok je tvrzení, o jehož pravdivosti lze jednoznačně rozhodnout.
O tom, jestli má být zapsán českými slovy, čínštinou, nebo matematickými symboly tato "definice" nic neříká.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#3 26. 06. 2009 08:27 — Editoval BrozekP (26. 06. 2009 08:32)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Definice výroku
↑ halogan:
V učebnici Matematika pro gymnázia - Základní poznatky z matematiky je uvedeno: "Výrokem se rozumí sdělení, u něhož má smysl otázka, zda je, či není pravdivé." Je tam i uveden příklad výroku  . My jsme se učili podle této učebnice a nikdo nám netvrdil, že by výrok nemohl být zapsán matematickými symboly.
. My jsme se učili podle této učebnice a nikdo nám netvrdil, že by výrok nemohl být zapsán matematickými symboly.
Je tam ale také uvedené, že např. 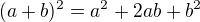 není samo o sobě výrok, dokud neuvedeme, co je a a b. Tak jestli nemohlo dojít k zaměnění těchto dvou věcí...
není samo o sobě výrok, dokud neuvedeme, co je a a b. Tak jestli nemohlo dojít k zaměnění těchto dvou věcí...
Offline
#5 26. 06. 2009 11:59
Re: Definice výroku
Ja, jako milovnik formalnich logik, si dovolim malou poznamku. Tusim, ze jsem nekde cetl primo formalni defnici vyroku (formalni tim, ze se neodkazuje ne zadne nematematicke pojmy jako "oznamovaci veta"), ale ted si ne ni nemuzu zaboha vzpomenout.
Ja bych jako vyrok chapal kazdou syntakticky spravnou formuli vyrokove, predikatove ci jakekoliv jine logiky. Tam totiz mame presnou definici toho, co je to formule a co presne znamena, ze je pravdiva.
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline